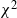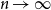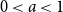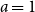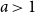Refine search
Actions for selected content:
502 results
THE NUMBER OF PARTS IN A RANDOM t-REGULAR PARTITION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 16 October 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Large and moderate deviations for Gaussian neural networks
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 01 October 2025, pp. 1-20
-
- Article
- Export citation
Limit theorems for the number of crossings and stress in projections of a random geometric graph
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 01 October 2025, pp. 1-24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quasi-stationary distributions for subcritical branching Markov chains
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 10 September 2025, pp. 1-47
-
- Article
- Export citation
Asymptotic mixed normality of maximum-likelihood estimator for Ewens–Pitman partition
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limit theorems for a class of unbounded observables with an application to ‘Sampling the Lindelöf hypothesis’
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 12 August 2025, pp. 1-59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Convergence of the QuickVal residual
- Part of
-
- Journal:
- Combinatorics, Probability and Computing , First View
- Published online by Cambridge University Press:
- 11 August 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Ergodic properties of the Hawkes process with a general excitation kernel
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 30 June 2025, pp. 1-24
-
- Article
- Export citation
Stein’s method for distributions modelling competing and complementary risk problems
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 23 June 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sojourn functionals of time-dependent
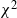 $\chi^2$-random fields on two-point homogeneous spaces
$\chi^2$-random fields on two-point homogeneous spaces
- Part of
-
- Journal:
- Journal of Applied Probability , First View
- Published online by Cambridge University Press:
- 13 June 2025, pp. 1-20
-
- Article
- Export citation
Steady-state Dirichlet approximation of the Wright-Fisher model using the prelimit generator comparison approach of Stein’s method
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 27 May 2025, pp. 1-39
-
- Article
- Export citation
Stable functional CLT for deterministic systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 26 May 2025, pp. 3192-3222
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limit laws for the generalized Zagreb indices of random graphs
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 26 May 2025, pp. 1-20
-
- Article
- Export citation
Exponentially preferential trees
- Part of
-
- Journal:
- Network Science / Volume 13 / 2025
- Published online by Cambridge University Press:
- 14 April 2025, e5
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A central limit theorem for jump diffusion processes in the presence of round-off errors
- Part of
-
- Journal:
- Advances in Applied Probability , First View
- Published online by Cambridge University Press:
- 25 March 2025, pp. 1-39
-
- Article
- Export citation
Graph connectivity with fixed endpoints in the random-connection model
- Part of
-
- Journal:
- Probability in the Engineering and Informational Sciences / Volume 39 / Issue 3 / July 2025
- Published online by Cambridge University Press:
- 21 February 2025, pp. 370-396
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Probabilistic voting models with varying speeds of Correlation decay
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 17 February 2025, pp. 35-64
- Print publication:
- March 2025
-
- Article
- Export citation
Edge Statistics for Lozenge Tilings of Polygons, II: Airy Line Ensemble
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 12 February 2025, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Interacting urns on directed networks with node-dependent sampling and reinforcement
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 62 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 972-996
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
QUENCHED CENTRAL LIMIT THEOREM FOR DVORETZKY COVERING
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 28 January 2025, pp. 368-378
- Print publication:
- April 2025
-
- Article
- Export citation