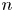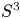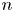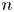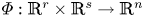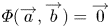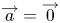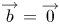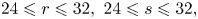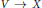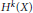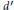Refine search
Actions for selected content:
11 results
BALANCING STRUCTURE AND DYNAMICS: DYNAMICAL NETWORKS AND EMBEDDING AS A MODELLING PARADIGM
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
 $\mathbb {Z}$-disks in
$\mathbb {Z}$-disks in  ${\mathbb {C}} P^2$
${\mathbb {C}} P^2$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 6 / June 2025
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1357-1403
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Embedding spheres in knot traces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 10 / October 2021
- Published online by Cambridge University Press:
- 20 October 2021, pp. 2242-2279
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonsingular bilinear maps revisited
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 17 March 2020, pp. 377-390
- Print publication:
- February 2021
-
- Article
- Export citation
EMBEDDINGS, NORMAL INVARIANTS AND FUNCTOR CALCULUS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 225 / March 2017
- Published online by Cambridge University Press:
- 19 August 2016, pp. 152-184
- Print publication:
- March 2017
-
- Article
-
- You have access
- HTML
- Export citation
ON THE MAPPING CLASS GROUP OF A HEEGAARD SPLITTING
-
- Journal:
- Glasgow Mathematical Journal / Volume 56 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 13 August 2013, pp. 93-101
- Print publication:
- January 2014
-
- Article
-
- You have access
- Export citation
STRONG JORDAN SEPARATION AND APPLICATIONS TO RIGIDITY
-
- Journal:
- Journal of the London Mathematical Society / Volume 73 / Issue 3 / June 2006
- Published online by Cambridge University Press:
- 16 June 2006, pp. 681-700
- Print publication:
- June 2006
-
- Article
- Export citation
Embedding Coverings in Bundles
-
- Journal:
- Canadian Mathematical Bulletin / Volume 42 / Issue 1 / 01 March 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 52-55
- Print publication:
- 01 March 1999
-
- Article
-
- You have access
- Export citation
Which 3-Manifolds Embed in Triod × I × I?
-
- Journal:
- Canadian Mathematical Bulletin / Volume 40 / Issue 3 / 01 September 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 370-375
- Print publication:
- 01 September 1997
-
- Article
-
- You have access
- Export citation
Embedding Uncountably Many Mutually Exclusive Continua into Euclidean Space
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 2 / 01 June 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 207-214
- Print publication:
- 01 June 1989
-
- Article
-
- You have access
- Export citation
When are Immersions Diffeomorphisms?
-
- Journal:
- Canadian Mathematical Bulletin / Volume 24 / Issue 4 / 01 December 1981
- Published online by Cambridge University Press:
- 20 November 2018, pp. 491-492
- Print publication:
- 01 December 1981
-
- Article
-
- You have access
- Export citation