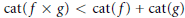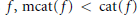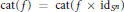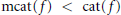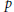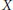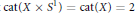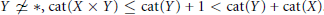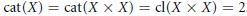Refine search
Actions for selected content:
22 results
Deloopings of Hurwitz spaces
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 7 / July 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 1651-1714
- Print publication:
- July 2024
-
- Article
- Export citation
Degrees of maps and multiscale geometry
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 January 2024, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The stable cohomology of self-equivalences of connected sums of products of spheres
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 05 January 2024, e1
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A
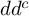 $dd^c$-TYPE CONDITION BEYOND THE KÄHLER REALM
$dd^c$-TYPE CONDITION BEYOND THE KÄHLER REALM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 28 November 2023, pp. 1651-1704
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A strictly commutative model for the cochain algebra of a space
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 12 October 2020, pp. 1718-1743
- Print publication:
- August 2020
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LOCAL SYSTEMS ON COMPLEMENTS OF ARRANGEMENTS OF SMOOTH, COMPLEX ALGEBRAIC HYPERSURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 6 / 2018
- Published online by Cambridge University Press:
- 23 May 2018, e6
-
- Article
-
- You have access
- Open access
- Export citation
Rational Models of the Complement of a Subpolyhedron in a Manifold with Boundary
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 2 / 01 April 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 265-293
- Print publication:
- 01 April 2018
-
- Article
-
- You have access
- Export citation
RANK TWO TOPOLOGICAL AND INFINITESIMAL EMBEDDED JUMP LOCI OF QUASI-PROJECTIVE MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 2 / March 2020
- Published online by Cambridge University Press:
- 15 February 2018, pp. 451-485
- Print publication:
- March 2020
-
- Article
- Export citation
Maurer–Cartan Elements in the Lie Models of Finite Simplicial Complexes
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 3 / 01 September 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 470-477
- Print publication:
- 01 September 2017
-
- Article
-
- You have access
- Export citation
Daniel Quillen, the father of abstract homotopy theory
-
- Journal:
- Journal of K-Theory / Volume 11 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 01 March 2013, pp. 479-491
- Print publication:
- June 2013
-
- Article
- Export citation
The Ranks of the Homotopy Groups of a Finite Dimensional Complex
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 1 / 01 February 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 82-119
- Print publication:
- 01 February 2013
-
- Article
-
- You have access
- Export citation
Algebraic and topological aspects of the schematization functor
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 633-686
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation
Schematic homotopy types and non-abelian Hodge theory
- Part of
-
- Journal:
- Compositio Mathematica / Volume 144 / Issue 3 / May 2008
- Published online by Cambridge University Press:
- 01 May 2008, pp. 582-632
- Print publication:
- May 2008
-
- Article
-
- You have access
- Export citation
the cohomology algebra of unordered configuration spaces
-
- Journal:
- Journal of the London Mathematical Society / Volume 72 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 04 October 2005, pp. 525-544
- Print publication:
- October 2005
-
- Article
- Export citation
Equivariant Formality for Actions of Torus Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 6 / 01 December 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1290-1307
- Print publication:
- 01 December 2004
-
- Article
-
- You have access
- Export citation
The rational topology of gauge groups and of spaces of connections
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 01 December 2004, pp. 262-270
- Print publication:
- January 2005
-
- Article
-
- You have access
- Export citation
On the Lusternik-Schnirelmann Category of Maps
-
- Journal:
- Canadian Journal of Mathematics / Volume 54 / Issue 3 / 01 June 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 608-633
- Print publication:
- 01 June 2002
-
- Article
-
- You have access
- Export citation
Algèbres quasi-commutatives et carrés de Steenrod
-
- Journal:
- Canadian Journal of Mathematics / Volume 51 / Issue 1 / 01 February 1999
- Published online by Cambridge University Press:
- 20 November 2018, pp. 49-68
- Print publication:
- 01 February 1999
-
- Article
-
- You have access
- Export citation
Lusternik-Schnirelmann Category and Algebraic R-Local Homotopy Theory
-
- Journal:
- Canadian Journal of Mathematics / Volume 50 / Issue 4 / 01 August 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 845-862
- Print publication:
- 01 August 1998
-
- Article
-
- You have access
- Export citation
Rational Classification of Simple Function Space Components for Flag Manifolds
-
- Journal:
- Canadian Journal of Mathematics / Volume 49 / Issue 4 / 01 August 1997
- Published online by Cambridge University Press:
- 20 November 2018, pp. 855-864
- Print publication:
- 01 August 1997
-
- Article
-
- You have access
- Export citation
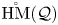
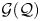
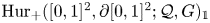
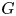
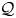
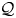
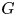
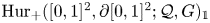
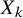
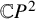
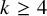
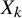
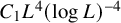
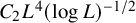
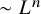
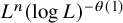
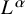
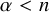

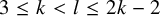
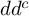
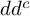
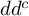
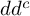
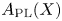
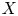
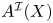
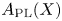
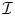
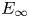
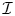
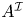
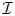
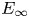
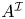
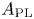
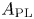
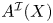
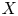
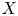
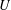
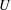
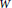
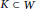
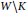
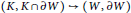
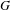
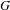
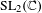
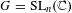
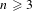
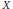
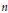
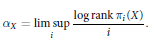
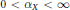
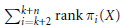
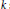
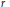
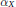
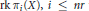
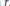
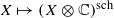 , introduced by the third author as a substitute for the rationalization functor in homotopy theory in the case of non-simply connected spaces. Our main result is the construction of a
, introduced by the third author as a substitute for the rationalization functor in homotopy theory in the case of non-simply connected spaces. Our main result is the construction of a 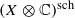 . This Hodge decomposition is encoded in an action of the discrete group
. This Hodge decomposition is encoded in an action of the discrete group 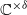 on the object
on the object