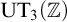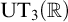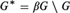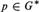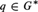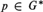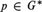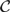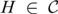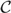Refine search
Actions for selected content:
26 results
Twisted Rokhlin property for mapping class groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 02 September 2025, pp. 1-23
-
- Article
- Export citation
Echeloned Spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On Thompson groups for Ważewski dendrites
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 1 / July 2025
- Published online by Cambridge University Press:
- 19 May 2025, pp. 189-231
- Print publication:
- July 2025
-
- Article
- Export citation
The weak Ramsey property and extreme amenability
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 11 November 2024, e96
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE SHAPE OF COMPACT COVERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 October 2024, pp. 1-15
-
- Article
- Export citation
Invariant Ideal Axiom
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 20 May 2022, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOHR COMPACTIFICATIONS OF GROUPS AND RINGS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 88 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 04 February 2022, pp. 1103-1137
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AUTOMATIC CONTINUITY FOR ISOMETRY GROUPS – ERRATUM
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 02 February 2021, pp. 2253-2255
- Print publication:
- November 2022
-
- Article
- Export citation
ON THE AUTOMORPHISM GROUP OF THE UNIVERSAL HOMOGENEOUS MEET-TREE
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 86 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 01 February 2021, pp. 1508-1540
- Print publication:
- December 2021
-
- Article
- Export citation
Expansive dynamics on locally compact groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 18 November 2020, pp. 3768-3779
- Print publication:
- December 2021
-
- Article
- Export citation
COHERENT EXTENSION OF PARTIAL AUTOMORPHISMS, FREE AMALGAMATION AND AUTOMORPHISM GROUPS
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 06 May 2019, pp. 199-223
- Print publication:
- March 2020
-
- Article
- Export citation
Actions of Semitopological Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 04 January 2019, pp. 441-450
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
ON GENERALISED METRISABILITY AND CARDINAL INVARIANTS IN QUASITOPOLOGICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 17 October 2018, pp. 302-310
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
On Følner sets in topological groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 7 / July 2018
- Published online by Cambridge University Press:
- 16 May 2018, pp. 1333-1361
- Print publication:
- July 2018
-
- Article
- Export citation
AUTOMATIC CONTINUITY FOR ISOMETRY GROUPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 18 / Issue 3 / May 2019
- Published online by Cambridge University Press:
- 11 April 2017, pp. 561-590
- Print publication:
- May 2019
-
- Article
- Export citation
LEFT MAXIMAL AND STRONGLY RIGHT MAXIMAL IDEMPOTENTS ING*
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 1 / March 2017
- Published online by Cambridge University Press:
- 21 March 2017, pp. 26-34
- Print publication:
- March 2017
-
- Article
- Export citation
ON VARIETIES OF ABELIAN TOPOLOGICAL GROUPS WITH COPRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 19 October 2016, pp. 54-65
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
CONSEQUENCES OF THE EXISTENCE OF AMPLE GENERICS AND AUTOMORPHISM GROUPS OF HOMOGENEOUS METRIC STRUCTURES
-
- Journal:
- The Journal of Symbolic Logic / Volume 81 / Issue 3 / September 2016
- Published online by Cambridge University Press:
- 14 September 2016, pp. 876-886
- Print publication:
- September 2016
-
- Article
- Export citation
UNIVERSAL SUBGROUPS OF POLISH GROUPS
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 12 December 2014, pp. 1148-1183
- Print publication:
- December 2014
-
- Article
- Export citation
New Examples of Small Polish Structures
-
- Journal:
- The Journal of Symbolic Logic / Volume 78 / Issue 3 / September 2013
- Published online by Cambridge University Press:
- 12 March 2014, pp. 969-976
- Print publication:
- September 2013
-
- Article
- Export citation