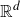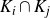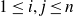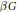Refine search
Actions for selected content:
10 results
Relative cell complexes in closure spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-9
-
- Article
- Export citation
The connectedness of Sierpiński sponges with rotational and reflectional components and associated graph-directed systems
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 2 / March 2025
- Published online by Cambridge University Press:
- 21 February 2025, pp. 133-156
- Print publication:
- March 2025
-
- Article
-
- You have access
- HTML
- Export citation
TAMING THE ‘ELSEWHERE’: ON EXPRESSIVITY OF TOPOLOGICAL LANGUAGES
- Part of
-
- Journal:
- The Review of Symbolic Logic / Volume 17 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 28 March 2022, pp. 144-153
- Print publication:
- March 2024
-
- Article
- Export citation
A TOPOLOGICAL VARIATION OF THE RECONSTRUCTION CONJECTURE
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 1 / January 2017
- Published online by Cambridge University Press:
- 10 June 2016, pp. 221-235
- Print publication:
- January 2017
-
- Article
-
- You have access
- Export citation
SHEAF RECURSION AND A SEPARATION THEOREM
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 18 August 2014, pp. 882-907
- Print publication:
- September 2014
-
- Article
- Export citation
Regular Homeomorphisms of Finite Order on Countable Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 3 / 01 June 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 708-720
- Print publication:
- 01 June 2009
-
- Article
-
- You have access
- Export citation
Relative Homotopy in Relational Structures
-
- Journal:
- Canadian Mathematical Bulletin / Volume 51 / Issue 2 / 01 June 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 310-320
- Print publication:
- 01 June 2008
-
- Article
-
- You have access
- Export citation
Connection Properties in Nearness Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 28 / Issue 2 / 01 June 1985
- Published online by Cambridge University Press:
- 20 November 2018, pp. 212-217
- Print publication:
- 01 June 1985
-
- Article
-
- You have access
- Export citation
Nearnesses and T0 -Extensions of Topological Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 26 / Issue 4 / 01 December 1983
- Published online by Cambridge University Press:
- 20 November 2018, pp. 430-437
- Print publication:
- 01 December 1983
-
- Article
-
- You have access
- Export citation
An Ultrafilter Completion of a Nearness Space
-
- Journal:
- Canadian Mathematical Bulletin / Volume 24 / Issue 1 / 01 March 1981
- Published online by Cambridge University Press:
- 20 November 2018, pp. 13-22
- Print publication:
- 01 March 1981
-
- Article
-
- You have access
- Export citation