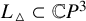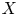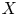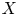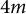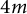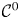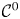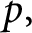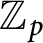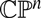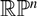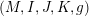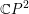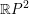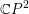Refine search
Actions for selected content:
23 results
Calabi–Yau structures on topological Fukaya categories
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1128-1214
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative quantum cohomology of the Chiang Lagrangian
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 17 March 2025, e56
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-Orientable Lagrangian Fillings of Legendrian Knots
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 27 September 2023, pp. 123-153
- Print publication:
- January 2024
-
- Article
- Export citation
Hamiltonian knottedness and lifting paths from the shape invariant
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 11 / November 2023
- Published online by Cambridge University Press:
- 18 September 2023, pp. 2416-2457
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on Lagrangian submanifolds in symplectic
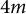 $4m$-manifolds
$4m$-manifolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 25 July 2022, pp. 525-531
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
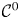 $\mathbb {\mathcal {C}}^{0}$-rigidity of Lagrangian submanifolds and punctured holomorphic disks in the cotangent bundle
$\mathbb {\mathcal {C}}^{0}$-rigidity of Lagrangian submanifolds and punctured holomorphic disks in the cotangent bundle
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 03 November 2021, pp. 2433-2493
- Print publication:
- November 2021
-
- Article
- Export citation
Tropically constructed Lagrangians in mirror quintic threefolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 20 November 2020, e58
-
- Article
-
- You have access
- Open access
- Export citation
Lagrangian foliations and Anosov symplectomorphisms on Kähler manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 3325-3335
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
Homology supported in Lagrangian submanifolds in mirror quintic threefolds
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 3 / September 2021
- Published online by Cambridge University Press:
- 11 September 2020, pp. 709-724
- Print publication:
- September 2021
-
- Article
- Export citation
Monotone Lagrangians in
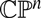 ${\mathbb{C}}{\mathbb{P}}^n$ of minimal Maslov number n + 1
${\mathbb{C}}{\mathbb{P}}^n$ of minimal Maslov number n + 1
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 1 / July 2021
- Published online by Cambridge University Press:
- 21 February 2020, pp. 1-21
- Print publication:
- July 2021
-
- Article
- Export citation
Locality in the Fukaya category of a hyperkähler manifold
- Part of
-
- Journal:
- Compositio Mathematica / Volume 155 / Issue 10 / October 2019
- Published online by Cambridge University Press:
- 06 September 2019, pp. 1924-1958
- Print publication:
- October 2019
-
- Article
- Export citation
A stability index for travelling waves in activator-inhibitor systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 517-548
- Print publication:
- February 2020
-
- Article
- Export citation
Lagrangian submanifolds of the nearly Kähler 𝕊3 × 𝕊3 from minimal surfaces in 𝕊3
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 655-689
- Print publication:
- June 2019
-
- Article
- Export citation
Dehn twist exact sequences through Lagrangian cobordism
- Part of
-
- Journal:
- Compositio Mathematica / Volume 154 / Issue 12 / December 2018
- Published online by Cambridge University Press:
- 05 November 2018, pp. 2485-2533
- Print publication:
- December 2018
-
- Article
- Export citation
A Real-analytic Nonpolynomially Convex Isotropic Torus with no Attached Discs
-
- Journal:
- Canadian Mathematical Bulletin / Volume 61 / Issue 2 / 01 June 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 289-291
- Print publication:
- 01 June 2018
-
- Article
-
- You have access
- Export citation
On an exotic Lagrangian torus in
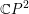 $\mathbb{C}P^{2}$
$\mathbb{C}P^{2}$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 151 / Issue 7 / July 2015
- Published online by Cambridge University Press:
- 27 February 2015, pp. 1372-1394
- Print publication:
- July 2015
-
- Article
- Export citation
ON BI-HARMONIC HYPERSURFACES IN EUCLIDEAN SPACE OF ARBITRARY DIMENSION
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 3 / September 2015
- Published online by Cambridge University Press:
- 18 December 2014, pp. 633-642
- Print publication:
- September 2015
-
- Article
-
- You have access
- Export citation
Bounding Lagrangian widths via geodesic paths
- Part of
-
- Journal:
- Compositio Mathematica / Volume 150 / Issue 12 / December 2014
- Published online by Cambridge University Press:
- 17 September 2014, pp. 2143-2183
- Print publication:
- December 2014
-
- Article
- Export citation
GEOMETRIC PHASES IN THE QUANTISATION OF BOSONS AND FERMIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 90 / Issue 2 / April 2011
- Published online by Cambridge University Press:
- 29 June 2011, pp. 221-235
- Print publication:
- April 2011
-
- Article
-
- You have access
- Export citation
Rigid subsets of symplectic manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 3 / May 2009
- Published online by Cambridge University Press:
- 01 May 2009, pp. 773-826
- Print publication:
- May 2009
-
- Article
-
- You have access
- Export citation