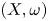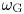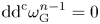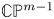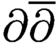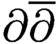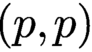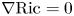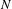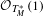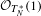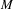Refine search
Actions for selected content:
47 results
COHOMOLOGY ISOMORPHISM OF SYMMETRIC POWER OF COTANGENT BUNDLE OF BALL QUOTIENT AND ITS TOROIDAL COMPACTIFICATION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 261 / 2026
- Published online by Cambridge University Press:
- 11 December 2025, e1
- Print publication:
- 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SPECIAL RICCI–HESSIAN EQUATIONS ON KÄHLER MANIFOLDS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 07 July 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
GAUSSIAN HOLOMORPHIC SECTIONS ON NONCOMPACT COMPLEX MANIFOLDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 12 March 2025, pp. 1197-1262
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOTT MANIFOLDS WITH VANISHING FUTAKI INVARIANTS FOR ALL KAHLER CLASSES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 259 / September 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 453-472
- Print publication:
- September 2025
-
- Article
- Export citation
CYT and SKT manifolds with parallel Bismut torsion
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 November 2024, pp. 1-26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Invariant scalar-flat Kähler metrics on line bundles over generalized flag varieties
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 13 May 2024, pp. 1611-1636
- Print publication:
- October 2025
-
- Article
- Export citation
Examples of dHYM connections in a variable background
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 02 October 2023, pp. 1609-1637
- Print publication:
- October 2024
-
- Article
- Export citation
On the pluriclosed flow on Oeljeklaus–Toma manifolds
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 27 December 2022, pp. 39-65
- Print publication:
- February 2024
-
- Article
- Export citation
Singular Gauduchon metrics
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 17 August 2022, pp. 1314-1328
- Print publication:
- June 2022
-
- Article
- Export citation
A note on holomorphic sectional curvature of a hermitian manifold
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 04 March 2022, pp. 739-745
- Print publication:
- September 2022
-
- Article
- Export citation
On cohomogeneity one Hermitian non-Kähler metrics
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 17 February 2022, pp. 545-587
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting and equidistribution in quaternionic Heisenberg groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 1 / July 2022
- Published online by Cambridge University Press:
- 08 July 2021, pp. 67-104
- Print publication:
- July 2022
-
- Article
- Export citation
POWER SERIES PROOFS FOR LOCAL STABILITIES OF KÄHLER AND BALANCED STRUCTURES WITH MILD
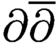 $\partial \overline {\partial }$-LEMMA
$\partial \overline {\partial }$-LEMMA
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 246 / June 2022
- Published online by Cambridge University Press:
- 08 June 2021, pp. 305-354
- Print publication:
- June 2022
-
- Article
- Export citation
Uniqueness of optimal symplectic connections
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 04 March 2021, e18
-
- Article
-
- You have access
- Open access
- Export citation
Non-existence of conformally flat real hypersurfaces in both the complex quadric and the complex hyperbolic quadric
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 15 February 2021, pp. 68-83
- Print publication:
- March 2022
-
- Article
- Export citation
A new classification on parallel Ricci tensor for real hypersurfaces in the complex quadric
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 18 November 2020, pp. 1846-1868
- Print publication:
- December 2021
-
- Article
- Export citation
RC-positive metrics on rationally connected manifolds
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 16 November 2020, e53
-
- Article
-
- You have access
- Open access
- Export citation
Lagrangian foliations and Anosov symplectomorphisms on Kähler manifolds
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 30 October 2020, pp. 3325-3335
- Print publication:
- November 2021
-
- Article
-
- You have access
- Open access
- Export citation
EXISTENCE AND COMPACTNESS THEORY FOR ALE SCALAR-FLAT KÄHLER SURFACES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 10 January 2020, e1
-
- Article
-
- You have access
- Open access
- Export citation
RC-POSITIVITY, VANISHING THEOREMS AND RIGIDITY OF HOLOMORPHIC MAPS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 11 October 2019, pp. 1023-1038
- Print publication:
- May 2021
-
- Article
- Export citation