Let (W, S) be a Coxeter system of rank n, and let $p_{(W, S)}(t)$ be its growth function. It is known that $p_{(W, S)}(q^{-1}) \lt \infty$ holds for all $n \leq q \in \mathbb{N}$. In this paper, we will show that this still holds for $q = n-1$, if (W, S) is 2-spherical. Moreover, we will prove that $p_{(W, S)}(q^{-1}) = \infty$ holds for $q = n-2$, if the Coxeter diagram of (W, S) is the complete graph. These two results provide a complete characterization of the finiteness of the growth function in the case of 2-spherical Coxeter systems with a complete Coxeter diagram.

Let W be a group endowed with a finite set S of generators. A representation $(V,\rho )$ of W is called a reflection representation of $(W,S)$ if $\rho (s)$ is a (generalized) reflection on V for each generator $s \in S$. In this article, we prove that for any irreducible reflection representation V, all the exterior powers $\bigwedge ^d V$, $d = 0, 1, \dots , \dim V$, are irreducible W-modules, and they are non-isomorphic to each other. This extends a theorem of R. Steinberg which is stated for Euclidean reflection groups. Moreover, we prove that the exterior powers (except for the 0th and the highest power) of two non-isomorphic reflection representations always give non-isomorphic W-modules. This allows us to construct numerous pairwise non-isomorphic irreducible representations for such groups, especially for Coxeter groups.

Given any smooth germ of a 3-fold flopping contraction, we first give a combinatorial characterisation of which Gopakumar–Vafa (GV) invariants are non-zero, by prescribing multiplicities to the walls in the movable cone. On the Gromov–Witten (GW) side, this allows us to describe, and even draw, the critical locus of the associated quantum potential. We prove that the critical locus is the infinite hyperplane arrangement of Iyama and the second author and, moreover, that the quantum potential can be reconstructed from a finite fundamental domain. We then iterate, obtaining a combinatorial description of the matrix that controls the transformation of the non-zero GV invariants under a flop. There are three main ingredients and applications: (1) a construction of flops from simultaneous resolution via cosets, which describes how the dual graph changes; (2) a closed formula, which describes the change in dimension of the contraction algebra under flop; and (3) a direct and explicit isomorphism between quantum cohomologies of different crepant resolutions, giving a Coxeter-style, visual proof of the Crepant Transformation Conjecture for isolated cDV singularities.

In 1968, Steinberg [Endomorphisms of Linear Algebraic Groups, Memoirs of the American Mathematical Society, 80 (American Mathematical Society, Providence, RI, 1968)] proved a theorem stating that the exterior powers of an irreducible reflection representation of a Euclidean reflection group are again irreducible and pairwise nonisomorphic. We extend this result to a more general context where the inner product invariant under the group action may not necessarily exist.

We classify all mutation-finite quivers with real weights. We show that every finite mutation class not originating from an integer skew-symmetrisable matrix has a geometric realisation by reflections. We also explore the structure of acyclic representatives in finite mutation classes and their relations to acute-angled simplicial domains in the corresponding reflection groups.

In this article, we establish an explicit correspondence between kissing reflection groups and critically fixed anti-rational maps. The correspondence, which is expressed using simple planar graphs, has several dynamical consequences. As an application of this correspondence, we give complete answers to geometric mating problems for critically fixed anti-rational maps.

We shall prove a convergence result relative to sequences of Minkowski symmetrals of general compact sets. In particular, we investigate the case when this process is induced by sequences of subspaces whose elements belong to a finite family, following the path marked by Klain in Klain (2012, Advances in Applied Mathematics 48, 340–353), and the generalizations in Bianchi et al. (2019, Convergence of symmetrization processes, preprint) and Bianchi et al. (2012, Indiana University Mathematics Journal 61, 1695–1710). We prove an analogous result for fiber symmetrization of a specific class of compact sets. The idempotency for symmetrizations of this family of sets is investigated, leading to a simple generalization of a result from Klartag (2004, Geometric and Functional Analysis 14, 1322–1338) regarding the approximation of a ball through a finite number of symmetrizations, and generalizing an approximation result in Fradelizi, Làngi and Zvavitch (2020, Volume of the Minkowski sums of star-shaped sets, preprint).

We prove a necessary and sufficient condition for the graded algebra of automorphic forms on a symmetric domain of type IV being free. From the necessary condition, we derive a classification result. Let $M$ be an even lattice of signature $(2,n)$ splitting two hyperbolic planes. Suppose $\Gamma$ is a subgroup of the integral orthogonal group of $M$ containing the discriminant kernel. It is proved that there are exactly 26 groups $\Gamma$ such that the space of modular forms for $\Gamma$ is a free algebra. Using the sufficient condition, we recover some well-known results.

In this paper, we investigate the set of accumulation points of normalized roots of infinite Coxeter groups for certain class of their action. Concretely, we prove the conjecture proposed in [6, Section 3.2] in the case where the equipped Coxeter matrices are of type $(n-1,1)$, where $n$ is the rank. Moreover, we obtain that the set of such accumulation points coincides with the closure of the orbit of one point of normalized limit roots. In addition, in order to prove our main results, we also investigate some properties on fixed points of the action.

Due to work of $\text{W}$ . Parry it is known that the growth rate of a hyperbolic Coxeter group acting cocompactly on ${{\mathbb{H}}^{3}}$ is a Salem number. This being the arithmetic situation, we prove that the simplex group (3,5,3) has the smallest growth rate among all cocompact hyperbolic Coxeter groups, and that it is, as such, unique. Our approach provides a different proof for the analog situation in ${{\text{H}}^{2}}$ where $\text{E}$ . Hironaka identified Lehmer's number as the minimal growth rate among all cocompact planar hyperbolic Coxeter groups and showed that it is (uniquely) achieved by the Coxeter triangle group (3,7).

Given a complete $\text{CAT}(0)$ space $X$ endowed with a geometric action of a group $\Gamma $ , it is known that if $\Gamma $ contains a free abelian group of rank $n$ , then $X$ contains a geometric flat of dimension $n$ . We prove the converse of this statement in the special case where $X$ is a convex subcomplex of the $\text{CAT}(0)$ realization of a Coxeter group $W$ , and $\Gamma $ is a subgroup of $W$ . In particular a convex cocompact subgroup of a Coxeter group is Gromov-hyperbolic if and only if it does not contain a free abelian group of rank 2. Our result also provides an explicit control on geometric flats in the $\text{CAT}(0)$ realization of arbitrary Tits buildings.

We describe the group of all reflection-preserving automorphisms of an imprimitive complex reflection group. We also study some properties of this automorphism group.

A star is a planar set of three lines through a common point in which the angle between each pair is 60∘.A set of lines through a point in which the angle between each pair of lines is 60 or 90∘ is star-closed if for every pair of its lines at 60∘ the set contains the third line of the star. In 1976 Cameron, Goethals, Seidel and Shult showed that the indecomposable star-closed sets in Euclidean space are the root systems of types An, Dn, E6, E7 and E8. This result was a key part of their determination of all graphs with least eigenvalue −2. Subsequently, Cvetković, Rowlinson and Simić determined all star-closed extensions of these line systems. We generalize this result on extensions of line systems to complex n-space equipped with a hermitian inner product. There is one further infinite family, and two exceptional types arising from Burkhardt and Mitchell’s complex reflection groups in dimensions five and six. The proof is a geometric version of Mitchell’s classification of complex reflection groups in dimensions greater than four.

Let G be a finite reflection group acting in a complex vector space V = ℂr , whose coordinate ring will be denoted by S. Any element γ ∈ GL(V) which normalises G acts on the ring SG of G-invariants. We attach invariants of the coset Gγ to this action, and show that if G′ is a parabolic subgroup of G, also normalised by γ, the invariants attaching to G′γ are essentially the same as those of Gγ. Four applications are given. First, we give a generalisation of a result of Springer-Stembridge which relates the module structures of the coinvariant algebras of G and G′ and secondly, we give a general criterion for an element of Gγ to be regular (in Springer’s sense) in invariant-theoretic terms, and use it to prove that up to a central element, all reflection cosets contain a regular element. Third, we prove the existence in any well-generated group, of analogues of Coxeter elements of the real reflection groups. Finally, we apply the analysis to quotients of G which are themselves reflection groups.

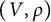
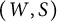
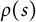
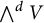
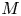
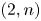
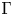
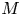
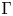
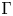
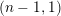
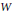
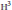
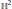
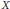
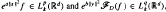In this paper, we give a generalization of Hardy's theorems for the Dunkl transform ℱD on ℝd. More precisely for all a > 0, b > 0 and p, q ∈ [1, + ∞], we determine the measurable functions f on ℝd such that where 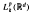are the Lebesgue spaces associated with the Dunkl transform.

The paper presents a construction of fibered links $(K, \Sigma)$ out of chord diagrams $\sL$. Let $\Gamma$ be the incidence graph of $\sL$. Under certain conditions on $\sL$ the symmetrized Seifert matrix of $(K, \Sigma)$ equals the bilinear form of the simply-laced Coxeter system $(W, S)$ associated to $\Gamma$; and the monodromy of $(K, \Sigma)$ equals minus the Coxeter element of $(W, S)$. Lehmer's problem is solved for the monodromy of these Coxeter links.

Let $G$ be a finite group generated by (pseudo-) reflections in a complex vector space and let $g$ be any linear transformation which normalises $G$ . In an earlier paper, the authors showed how to associate with any maximal eigenspace of an element of the coset $gG$ , a subquotient of $G$ which acts as a reflection group on the eigenspace. In this work, we address the questions of irreducibility and the coexponents of this subquotient, as well as centralisers in $G$ of certain elements of the coset. A criterion is also given in terms of the invariant degrees of $G$ for an integer to be regular for $G$ . A key tool is the investigation of extensions of invariant vector fields on the eigenspace, which leads to some results and questions concerning the geometry of intersections of invariant hypersurfaces.

For positive integers p and q with (p − 2)(q − 2) > 4 there is, in the hyperbolic plane, a group [p, q] generated by reflections in the three sides of a triangle ABC with angles π/p, π/q, π/2. Hyperbolic trigonometry shows that the side AC has length ψ, where cosh ψ = c/s, c = cos π/q, s = sin π/p. For a conformal drawing inside the unit circle with centre A, we may take the sides AB and AC to run straight along radiiwhile BC appears as an arc of a circle orthogonal to the unit circle. 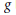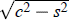The circle containing this arc is found to have radius 1/ sinh ψ = s/z, where z = , while its centre is at distance 1/ tanh ψ = c/z from A. In the hyperbolic triangle ABC, the altitude from AB to the right-angled vertex C is ζ, where sinh ζ = z.

It is shown that, in characteristic zero, a finite subgroup of a general linear group is generated by pseudo-reflections if and only if its ring of coinvariants satisfies Poincaré duality.

A complete answer is given to the question: Under what circumstances is the product of three harmonic homologies in PG(2, F) again a harmonic homology ? This is the natural question to ask in seeking a generalization to projective geometry of the Three Reflection Theorem of metric geometry. It is found that apart from two familiar special cases, and with one curious exception, the necessary and sufficient conditions on the harmonic homologies produce exactly the Three Reflection Theorem.