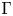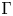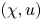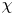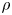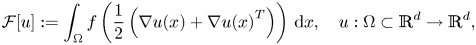Refine search
Actions for selected content:
33 results
Homogenization of vectorial free-discontinuity functionals with cohesive type surface terms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-71
-
- Article
- Export citation
Sobolev regularity of the inverse for minimizers of the neo-Hookean energy satisfying condition INV
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-21
-
- Article
- Export citation
Sufficiency of
 $\boldsymbol{c}$-cyclical monotonicity in a class of multi-marginal optimal transport problems
$\boldsymbol{c}$-cyclical monotonicity in a class of multi-marginal optimal transport problems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 36 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 14 May 2024, pp. 68-81
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp conditions for the validity of the Bourgain–Brezis–Mironescu formula
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 16 April 2024, pp. 1-24
-
- Article
- Export citation
On the lack of compactness in the axisymmetric neo-Hookean model
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 26 February 2024, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Non-local approximation of free-discontinuity problems in linear elasticity and application to stochastic homogenisation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 08 June 2023, pp. 1060-1094
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Extending linear growth functionals to functions of bounded fractional variation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 21 February 2023, pp. 304-327
- Print publication:
- February 2024
-
- Article
- Export citation
Pressure live loads and the variational derivation of linear elasticity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 09 December 2022, pp. 1929-1964
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relaxation for an optimal design problem in BD(Ω)
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 10 March 2022, pp. 721-763
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Γ-convergence and stochastic homogenization of degenerate integral functionals in weighted Sobolev spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 08 February 2022, pp. 491-544
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Brittle fracture in linearly elastic plates
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 19 November 2021, pp. 68-103
- Print publication:
- February 2023
-
- Article
- Export citation
Asymptotic variational analysis of incompressible elastic strings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 25 September 2020, pp. 1487-1514
- Print publication:
- October 2021
-
- Article
-
- You have access
- Open access
- Export citation
Continuity of solutions for the Δϕ-Laplacian operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 11 September 2020, pp. 1355-1382
- Print publication:
- August 2021
-
- Article
- Export citation
On a family of torsional creep problems in Finsler metrics
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 02 September 2020, pp. 24-41
- Print publication:
- February 2022
-
- Article
- Export citation
Minimizing movements for forced anisotropic mean curvature flow of partitions with mobilities
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 17 August 2020, pp. 1135-1170
- Print publication:
- August 2021
-
- Article
-
- You have access
- Open access
- Export citation
On the relaxation of integral functionals depending on the symmetrized gradient
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 08 April 2020, pp. 473-508
- Print publication:
- April 2021
-
- Article
- Export citation
The spectrum of the mean curvature operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 01 April 2020, pp. 451-463
- Print publication:
- April 2021
-
- Article
- Export citation
Quasiconvex relaxation of isotropic functions in incompressible planar hyperelasticity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 11 June 2019, pp. 2620-2631
- Print publication:
- October 2020
-
- Article
-
- You have access
- Open access
- Export citation
On c-cyclical monotonicity for optimal transport problem with Coulomb cost
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 30 / Issue 6 / December 2019
- Published online by Cambridge University Press:
- 23 May 2019, pp. 1210-1219
-
- Article
- Export citation
Nonlinear systems coupled through multi-marginal transport problems
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 29 April 2019, pp. 450-469
-
- Article
- Export citation