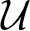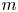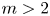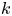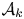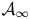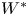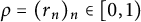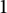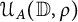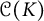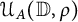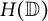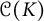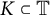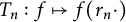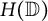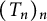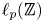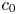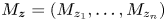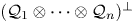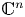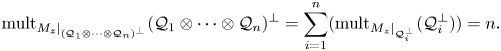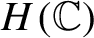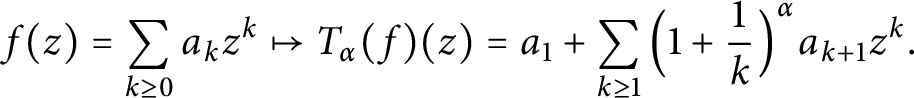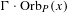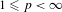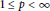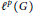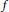Refine search
Actions for selected content:
31 results
Density properties of orbits for a hypercyclic operator on a Banach space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 18 July 2025, pp. 1-16
-
- Article
- Export citation
Hereditarily frequently hypercyclic operators and disjoint frequent hypercyclicity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 16 April 2025, pp. 3021-3072
- Print publication:
- October 2025
-
- Article
- Export citation
Zero-one law of orbital limit points for weighted shifts
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 07 April 2025, pp. 945-978
-
- Article
- Export citation
On several dynamical properties of shifts acting on directed trees
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-30
-
- Article
- Export citation
Growth of hypercyclic functions: a continuous path between
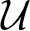 $\mathcal{U}$-frequent hypercyclicity and hypercyclicity
$\mathcal{U}$-frequent hypercyclicity and hypercyclicity
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 08 May 2024, pp. 794-829
-
- Article
- Export citation
Disjoint hypercyclicity, Sidon sets and weakly mixing operators
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 1315-1329
- Print publication:
- May 2024
-
- Article
- Export citation
Weakly concave operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 18 January 2023, pp. 1-32
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Abel universal functions
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 26 October 2022, pp. 1957-1985
- Print publication:
- December 2023
-
- Article
- Export citation
Chaos and frequent hypercyclicity for composition operators
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 04 June 2021, pp. 513-531
-
- Article
- Export citation
Multiplicities, invariant subspaces and an additive formula
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 2 / May 2021
- Published online by Cambridge University Press:
- 30 April 2021, pp. 279-297
-
- Article
- Export citation
INVERSE OF FREQUENTLY HYPERCYCLIC OPERATORS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 04 February 2021, pp. 1867-1886
- Print publication:
- November 2022
-
- Article
- Export citation
Mixing operators with prescribed unimodular eigenvalues
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 1 / January 2022
- Published online by Cambridge University Press:
- 28 December 2020, pp. 1-8
- Print publication:
- January 2022
-
- Article
- Export citation
Chaos and frequent hypercyclicity for weighted shifts
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 12 / December 2021
- Published online by Cambridge University Press:
- 28 December 2020, pp. 3634-3670
- Print publication:
- December 2021
-
- Article
- Export citation
Growth of frequently hypercyclic functions for some weighted Taylor shifts on the unit disc
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 11 June 2020, pp. 264-281
- Print publication:
- June 2021
-
- Article
- Export citation
Orbits of homogeneous polynomials on Banach spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 6 / June 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 1627-1655
- Print publication:
- June 2021
-
- Article
- Export citation
Shadowing and structural stability for operators
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 4 / April 2021
- Published online by Cambridge University Press:
- 10 January 2020, pp. 961-980
- Print publication:
- April 2021
-
- Article
- Export citation
Frequent universality criterion and densities
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 3 / March 2021
- Published online by Cambridge University Press:
- 25 November 2019, pp. 846-868
- Print publication:
- March 2021
-
- Article
- Export citation
FREQUENTLY HYPERCYCLIC BILATERAL SHIFTS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 61 / Issue 2 / May 2019
- Published online by Cambridge University Press:
- 20 June 2018, pp. 271-286
- Print publication:
- May 2019
-
- Article
-
- You have access
- Export citation
Disjoint Hypercyclicity and Weighted Translations on Discrete Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 4 / 01 December 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 712-720
- Print publication:
- 01 December 2017
-
- Article
-
- You have access
- Export citation
Functions Universal for all Translation Operators in Several Complex Variables
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 3 / 01 September 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 462-469
- Print publication:
- 01 September 2017
-
- Article
-
- You have access
- Export citation