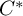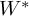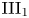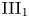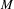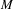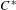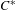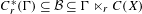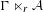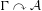Refine search
Actions for selected content:
57 results
PROPERTY (T) AND STRONG 1-BOUNDEDNESS FOR VON NEUMANN ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-34
-
- Article
- Export citation
Semigroups of self-similar actions and higher rank Baumslag–Solitar semigroups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 August 2025, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
QUANTUM EXPANDERS AND QUANTIFIER REDUCTION FOR TRACIAL VON NEUMANN ALGEBRAS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 04 July 2025, pp. 1-37
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Elementary equivalence and disintegration of tracial von Neumann algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 02 July 2025, e105
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RELATIVE POSITION BETWEEN A PAIR OF SPIN MODEL SUBFACTORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 1-38
- Print publication:
- August 2025
-
- Article
- Export citation
Products of commutators in matrix rings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 14 January 2025, pp. 512-529
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Isometric dilations for representations of product systems
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 28 November 2024, pp. 1-42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RIGIDITY FOR VON NEUMANN ALGEBRAS OF GRAPH PRODUCT GROUPS II. SUPERRIGIDITY RESULTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 117-156
- Print publication:
- January 2025
-
- Article
- Export citation
Asymptotic freeness in tracial ultraproducts
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 28 October 2024, e88
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Haagerup and Størmer's conjecture on pointwise inner automorphisms
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 10 / October 2024
- Published online by Cambridge University Press:
- 04 November 2024, pp. 2480-2495
- Print publication:
- October 2024
-
- Article
- Export citation
Corrigendum: Von Neumann algebras and extensions of inverse semigroups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 919-922
-
- Article
-
- You have access
- HTML
- Export citation
Measure equivalence rigidity via s-malleable deformations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 14 August 2023, pp. 2023-2050
- Print publication:
- October 2023
-
- Article
- Export citation
Poisson boundaries of II1 factors
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 8 / August 2022
- Published online by Cambridge University Press:
- 04 October 2022, pp. 1746-1776
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RIESZ TRANSFORMS ON COMPACT QUANTUM GROUPS AND STRONG SOLIDITY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 26 April 2021, pp. 2135-2171
- Print publication:
- November 2022
-
- Article
-
- You have access
- Open access
- Export citation
Lattice isomorphisms between projection lattices of von Neumann algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 13 November 2020, e49
-
- Article
-
- You have access
- Open access
- Export citation
CENTRAL SEQUENCES IN SUBHOMOGENEOUS UNITAL C*-ALGEBRAS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 2 / April 2021
- Published online by Cambridge University Press:
- 02 October 2020, pp. 318-325
- Print publication:
- April 2021
-
- Article
- Export citation
On the von Neumann algebras associated to Yang–Baxter operators
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 28 August 2020, pp. 1331-1354
- Print publication:
- August 2021
-
- Article
- Export citation
INNER AMENABLE GROUPOIDS AND CENTRAL SEQUENCES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 26 May 2020, e29
-
- Article
-
- You have access
- Open access
- Export citation
II1 FACTORS WITH EXOTIC CENTRAL SEQUENCE ALGEBRAS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 20 / Issue 5 / September 2021
- Published online by Cambridge University Press:
- 19 December 2019, pp. 1671-1696
- Print publication:
- September 2021
-
- Article
- Export citation
On simplicity of intermediate
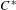 $C^{\ast }$-algebras
$C^{\ast }$-algebras
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 12 / December 2020
- Published online by Cambridge University Press:
- 06 June 2019, pp. 3181-3187
- Print publication:
- December 2020
-
- Article
- Export citation