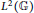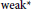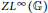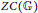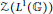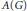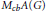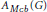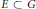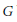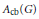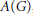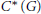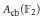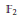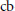Refine search
Actions for selected content:
7 results
Character Density in Central Subalgebras of Compact Quantum Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 3 / 01 September 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-461
- Print publication:
- 01 September 2017
-
- Article
-
- You have access
- Export citation
Norm One Idempotent cb-Multipliers with Applications to the Fourier Algebra in the cb-Multiplier Norm
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 4 / 01 December 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 654-662
- Print publication:
- 01 December 2011
-
- Article
-
- You have access
- Export citation
Operator Amenability of the Fourier Algebra in the cb-Multiplier Norm
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 5 / 01 October 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 966-980
- Print publication:
- 01 October 2007
-
- Article
-
- You have access
- Export citation
Homomorphisms of the algebra of locally integrable functions on the half line
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 81 / Issue 2 / October 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 253-278
- Print publication:
- October 2006
-
- Article
-
- You have access
- Export citation
SIMPLICIAL HOMOLOGY AND HOCHSCHILD COHOMOLOGY OF BANACH SEMILATTICE ALGEBRAS
-
- Journal:
- Glasgow Mathematical Journal / Volume 48 / Issue 2 / May 2006
- Published online by Cambridge University Press:
- 23 August 2006, pp. 231-245
- Print publication:
- May 2006
-
- Article
-
- You have access
- Export citation
AN ALMOST PRIME ELEMENT IN A COMMUTATIVE RADICAL BANACH ALGEBRA
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 37 / Issue 4 / August 2005
- Published online by Cambridge University Press:
- 02 August 2005, pp. 613-620
- Print publication:
- August 2005
-
- Article
- Export citation
The Operator Amenability of Uniform Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 46 / Issue 4 / 01 December 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 632-634
- Print publication:
- 01 December 2003
-
- Article
-
- You have access
- Export citation