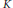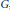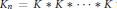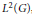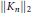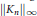Refine search
Actions for selected content:
11 results
Non-commutative skew-product extension dynamical systems
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 2672-2694
- Print publication:
- September 2025
-
- Article
- Export citation
The John–Nirenberg Inequality for the Regularized BLO Space on Non-homogeneous Metric Measure Spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 10 December 2019, pp. 643-654
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
BMO-Estimates for Maximal Operators via Approximations of the Identity with Non-Doubling Measures
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 6 / 14 December 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1419-1434
- Print publication:
- 14 December 2010
-
- Article
-
- You have access
- Export citation
WEIGHTED ESTIMATES FOR SINGULAR INTEGRAL OPERATORS WITH NONSMOOTH KERNELS AND APPLICATIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 85 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 377-417
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation
Generalized hypergroups and orthogonal polynomials
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 82 / Issue 3 / June 2007
- Published online by Cambridge University Press:
- 09 April 2009, pp. 369-394
- Print publication:
- June 2007
-
- Article
-
- You have access
- Export citation
Harmonic Analysis on Metrized Graphs
-
- Journal:
- Canadian Journal of Mathematics / Volume 59 / Issue 2 / 01 April 2007
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-275
- Print publication:
- 01 April 2007
-
- Article
-
- You have access
- Export citation
Some new Besov and Triebel-Lizorkin spaces associated with para-accretive functions on spaces of homogeneous type
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 80 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 09 April 2009, pp. 229-262
- Print publication:
- April 2006
-
- Article
-
- You have access
- Export citation
Some Conditions for Decay of Convolution Powers and Heat Kernels on Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 57 / Issue 6 / 01 December 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1193-1214
- Print publication:
- 01 December 2005
-
- Article
-
- You have access
- Export citation
Local hardy and BMO spaces on non-homogeneous spaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 79 / Issue 2 / October 2005
- Published online by Cambridge University Press:
- 09 April 2009, pp. 149-182
- Print publication:
- October 2005
-
- Article
-
- You have access
- Export citation
Calderón-type reproducing formulae on Lipschitz curves and surfaces
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 33-46
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
Embedding Theorems in Group C*-Algebras†
-
- Journal:
- Canadian Mathematical Bulletin / Volume 26 / Issue 2 / 01 June 1983
- Published online by Cambridge University Press:
- 20 November 2018, pp. 157-166
- Print publication:
- 01 June 1983
-
- Article
-
- You have access
- Export citation








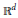
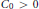
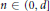
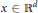
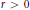
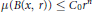
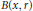


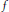
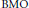
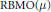
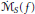
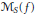

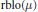
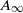 weights are established for singular integral operators with nonsmooth kernels via a new sharp maximal operator associated with a generalized approximation to the identity. As applications, the weighted
weights are established for singular integral operators with nonsmooth kernels via a new sharp maximal operator associated with a generalized approximation to the identity. As applications, the weighted