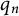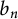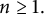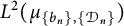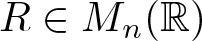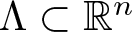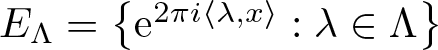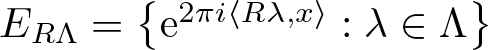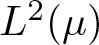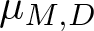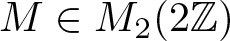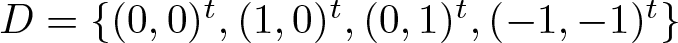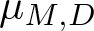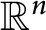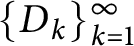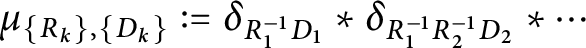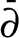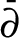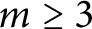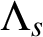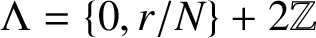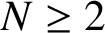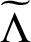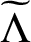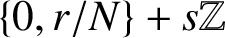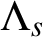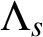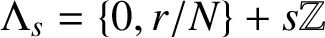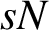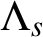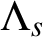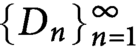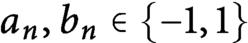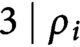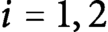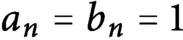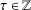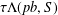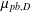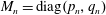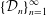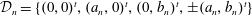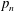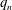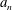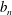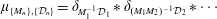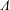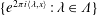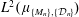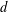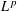Refine search
Actions for selected content:
48 results
THE SPECTRAL EIGENVALUES OF A CLASS OF PRODUCT-FORM SELF-SIMILAR SPECTRAL MEASURE
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 21 July 2025, pp. 246-263
- Print publication:
- October 2025
-
- Article
- Export citation
Superelliptic Affine Lie algebras and orthogonal polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 July 2025, e120
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Moment-SOS hierarchy: Applications and related topics
- Part of
-
- Journal:
- Acta Numerica / Volume 33 / July 2024
- Published online by Cambridge University Press:
- 04 September 2024, pp. 841-908
-
- Article
- Export citation
Tree structure of spectra of spectral Moran measures with consecutive digits
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 22 December 2023, pp. 593-610
- Print publication:
- September 2024
-
- Article
- Export citation
The spectral eigenmatrix problems of planar self-affine measures with four digits
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 897-918
-
- Article
- Export citation
Spectral analysis of bilateral birth–death processes: some new explicit examples
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 54 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 15 June 2022, pp. 1193-1221
- Print publication:
- December 2022
-
- Article
- Export citation
Spectrality of a class of Moran measures on
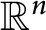 $\mathbb {R}^{n}$ with consecutive digit sets
$\mathbb {R}^{n}$ with consecutive digit sets
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 13 April 2022, pp. 269-285
- Print publication:
- March 2023
-
- Article
- Export citation
SPECTRAL INEQUALITIES FOR COMBINATIONS OF HERMITE FUNCTIONS AND NULL-CONTROLLABILITY FOR EVOLUTION EQUATIONS ENJOYING GELFAND–SHILOV SMOOTHING EFFECTS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 21 March 2022, pp. 2533-2582
- Print publication:
- November 2023
-
- Article
- Export citation
On smooth perturbations of Chebyshëv polynomials and
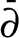 $ \bar {\partial } $-Riemann–Hilbert method
$ \bar {\partial } $-Riemann–Hilbert method
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 24 February 2022, pp. 142-155
- Print publication:
- March 2023
-
- Article
- Export citation
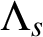 $\Lambda _s$-NONUNIFORM MULTIRESOLUTION ANALYSIS
$\Lambda _s$-NONUNIFORM MULTIRESOLUTION ANALYSIS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 23 November 2021, pp. 359-377
- Print publication:
- June 2023
-
- Article
- Export citation
Spectrality of Moran Sierpinski-type measures on
 ${\mathbb R}^2$
${\mathbb R}^2$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 18 January 2021, pp. 1024-1040
- Print publication:
- December 2021
-
- Article
- Export citation
NUMBER THEORY PROBLEMS RELATED TO THE SPECTRUM OF CANTOR-TYPE MEASURES WITH CONSECUTIVE DIGITS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 10 June 2020, pp. 113-123
- Print publication:
- February 2021
-
- Article
- Export citation
Spectrality of a Class of Moran Measures
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 17 January 2020, pp. 366-381
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
ODD–EVEN DECOMPOSITION OF FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 1 / August 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 104-108
- Print publication:
- August 2020
-
- Article
-
- You have access
- Export citation
Non-spectral Problem for Some Self-similar Measures
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 28 August 2019, pp. 318-327
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
ANALYSIS IN THE MULTI-DIMENSIONAL BALL
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 2 / 2019
- Published online by Cambridge University Press:
- 31 October 2018, pp. 190-212
- Print publication:
- 2019
-
- Article
- Export citation
Stochastic LU factorizations, Darboux transformations and urn models
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 55 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 16 November 2018, pp. 862-886
- Print publication:
- September 2018
-
- Article
- Export citation
Sparse Recovery via ℓq -Minimization for Polynomial Chaos Expansions
- Part of
-
- Journal:
- Numerical Mathematics: Theory, Methods and Applications / Volume 10 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 12 September 2017, pp. 775-797
- Print publication:
- November 2017
-
- Article
- Export citation
Strong Asymptotics of Hermite-PadéApproximants for Angelesco Systems
-
- Journal:
- Canadian Journal of Mathematics / Volume 68 / Issue 5 / 01 October 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1159-1200
- Print publication:
- 01 October 2016
-
- Article
-
- You have access
- Export citation
Multiple Spectra of Bernoulli Convolutions
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 60 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 10 May 2016, pp. 187-202
-
- Article
- Export citation