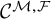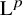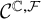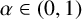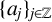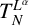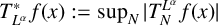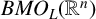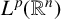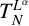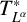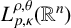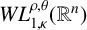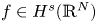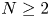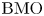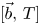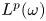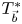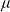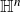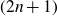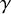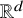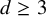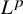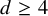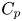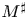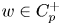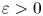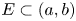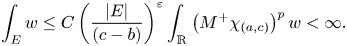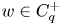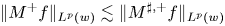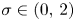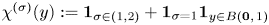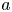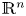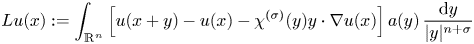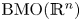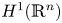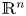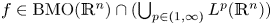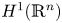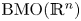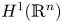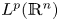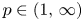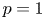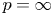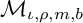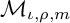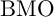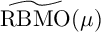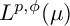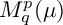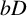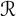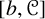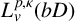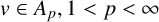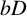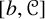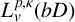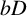Refine search
Actions for selected content:
110 results
ANALYSIS OF THE LAPLACIAN ON A CLASS OF NONDOUBLING CONNECTED SUMS AND MANIFOLDS WITH QUADRATICALLY DECAYING RICCI CURVATURE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 17 October 2025, pp. 1-2
-
- Article
-
- You have access
- HTML
- Export citation
Lorentz boundedness and compactness of Riesz transform commutator on stratified Lie groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-28
-
- Article
- Export citation
Parabolic Muckenhoupt weights characterized by parabolic fractional maximal and integral operators with time lag
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 17 March 2025, pp. 1-54
-
- Article
- Export citation
Boundedness on Triebel–Lizorkin spaces for the Calderón commutator with rough kernel
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 12 March 2025, pp. 1069-1081
- Print publication:
- December 2025
-
- Article
- Export citation
An endpoint estimate for product singular integral operators on stratified Lie groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 27 January 2025, pp. 1-32
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Parametric Fourier and Mellin transforms of power-constructible functions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 29 November 2024, e113
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOUNDEDNESS OF DIFFERENTIAL TRANSFORMS FOR FRACTIONAL HEAT SEMIGROUPS GENERATED BY SCHRÖDINGER OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 210-244
- Print publication:
- April 2025
-
- Article
- Export citation
Compact bilinear operators and paraproducts revisited
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 22 November 2024, pp. 44-59
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On restricted Falconer distance sets
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 05 February 2024, pp. 665-682
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp convergence for sequences of Schrödinger means and related generalizations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 25 September 2023, pp. 453-469
- Print publication:
- April 2025
-
- Article
- Export citation
Estimates for evolutionary partial differential equations in classical function spaces
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 01 September 2023, e76
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sharp Sobolev regularity of restricted X-ray transforms
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 30 August 2023, pp. 1583-1603
- Print publication:
- October 2024
-
- Article
- Export citation
SPECTRAL MULTIPLIER THEOREMS FOR ABSTRACT DIFFERENTIAL OPERATORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 29 June 2023, pp. 343-344
- Print publication:
- October 2023
-
- Article
-
- You have access
- HTML
- Export citation
The commutators of multilinear Calderón–Zygmund operators on weighted Hardy spaces
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 26 June 2023, pp. 1259-1280
- Print publication:
- August 2024
-
- Article
- Export citation
Necessary condition for the L2 boundedness of the Riesz transform on Heisenberg groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 2 / September 2023
- Published online by Cambridge University Press:
- 23 May 2023, pp. 445-458
- Print publication:
- September 2023
-
- Article
- Export citation
Sharp smoothing properties of averages over curves
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 10 February 2023, e4
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
One-sided $C_{p}$
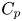 estimates via $M^{\sharp }$
estimates via $M^{\sharp }$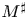 function
function
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 27 December 2022, pp. 2079-2105
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On BMO and Hardy regularity estimates for a class of non-local elliptic equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 14 December 2022, pp. 2025-2052
- Print publication:
- December 2023
-
- Article
- Export citation
FRACTIONAL TYPE MARCINKIEWICZ INTEGRAL AND ITS COMMUTATOR ON NONHOMOGENEOUS SPACES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 03 June 2022, pp. 801-822
- Print publication:
- December 2022
-
- Article
- Export citation
BOUNDEDNESS AND COMPACTNESS OF CAUCHY-TYPE INTEGRAL COMMUTATOR ON WEIGHTED MORREY SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 113 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 08 March 2022, pp. 36-56
- Print publication:
- August 2022
-
- Article
- Export citation