Refine search
Actions for selected content:
11 results
A Chebyshev-type alternation theorem for best approximation by a sum of two algebras
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 01 September 2023, pp. 971-978
-
- Article
- Export citation
Application of Reproducing Kernel Hilbert Spaces to a Minimization Problem with Prescribed Nodes
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 1 / Issue 4 / November 2011
- Published online by Cambridge University Press:
- 28 May 2015, pp. 372-378
- Print publication:
- November 2011
-
- Article
- Export citation
On L 1-Convergence of Fourier Series under the MVBV Condition
-
- Journal:
- Canadian Mathematical Bulletin / Volume 52 / Issue 4 / 01 December 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 627-636
- Print publication:
- 01 December 2009
-
- Article
-
- You have access
- Export citation
Automorphic Orthogonal and Extremal Polynomials
-
- Journal:
- Canadian Journal of Mathematics / Volume 55 / Issue 3 / 01 June 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 576-608
- Print publication:
- 01 June 2003
-
- Article
-
- You have access
- Export citation
Bivariate Polynomials of Least Deviation from Zero
-
- Journal:
- Canadian Journal of Mathematics / Volume 53 / Issue 3 / 01 June 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 489-505
- Print publication:
- 01 June 2001
-
- Article
-
- You have access
- Export citation
Variations on Müntz's Theme
-
- Journal:
- Canadian Mathematical Bulletin / Volume 34 / Issue 3 / 01 September 1991
- Published online by Cambridge University Press:
- 20 November 2018, pp. 305-310
- Print publication:
- 01 September 1991
-
- Article
-
- You have access
- Export citation
A Note on M-Ideals of Compact operators
-
- Journal:
- Canadian Mathematical Bulletin / Volume 32 / Issue 4 / 01 December 1989
- Published online by Cambridge University Press:
- 20 November 2018, pp. 434-440
- Print publication:
- 01 December 1989
-
- Article
-
- You have access
- Export citation
A Note on M-Summands in Dual Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 30 / Issue 4 / 01 December 1987
- Published online by Cambridge University Press:
- 20 November 2018, pp. 393-398
- Print publication:
- 01 December 1987
-
- Article
-
- You have access
- Export citation
On the Extreme Points of Quotients of L∞ by Douglas Algebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 27 / Issue 4 / 01 December 1984
- Published online by Cambridge University Press:
- 20 November 2018, pp. 517-522
- Print publication:
- 01 December 1984
-
- Article
-
- You have access
- Export citation
On Padé and Best Rational Approximation
-
- Journal:
- Canadian Mathematical Bulletin / Volume 26 / Issue 1 / 01 March 1983
- Published online by Cambridge University Press:
- 20 November 2018, pp. 50-57
- Print publication:
- 01 March 1983
-
- Article
-
- You have access
- Export citation
The Limit of Biased Varisolvent Chebyshev Approximation
-
- Journal:
- Canadian Mathematical Bulletin / Volume 25 / Issue 1 / 01 March 1982
- Published online by Cambridge University Press:
- 20 November 2018, pp. 54-58
- Print publication:
- 01 March 1982
-
- Article
-
- You have access
- Export citation
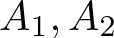
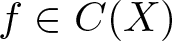
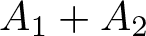
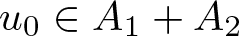
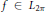
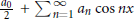
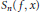
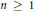

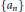
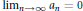
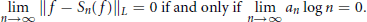
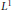
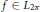
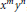
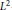
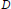
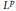
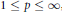
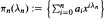 then the collection of spaces
then the collection of spaces 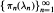 is dense in C[0,1] if and only if lim sup(log
is dense in C[0,1] if and only if lim sup(log 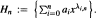 The derivations of these results require an examination of the location of the zeros of the associated Chebyshev polynomials.
The derivations of these results require an examination of the location of the zeros of the associated Chebyshev polynomials.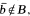 , there exists
, there exists 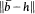 = 1 and h|
= 1 and h|