Refine search
Actions for selected content:
17 results
Discrete heat equation with irregular thermal conductivity and tempered distributional data
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 04 September 2023, pp. 57-80
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence of positive solutions for Kirchhoff-type problem in exterior domains
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 04 April 2023, pp. 182-217
-
- Article
- Export citation
Exponential decay for the KdV equation on ℝ with new localized dampings
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 4 / August 2023
- Published online by Cambridge University Press:
- 05 April 2022, pp. 1073-1098
- Print publication:
- August 2023
-
- Article
- Export citation
Jump phenomena of the n-th eigenvalue of discrete Sturm–Liouville problems with application to the continuous case
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 02 March 2022, pp. 619-653
- Print publication:
- April 2023
-
- Article
- Export citation
Perturbed Schrödinger lattice systems: existence of homoclinic solutions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1083-1096
- Print publication:
- August 2019
-
- Article
- Export citation
Integrable Properties of a Variant of the Discrete Hungry Toda Equations and Their Relationship to Eigenpairs of Band Matrices
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2018, pp. 785-798
- Print publication:
- November 2017
-
- Article
- Export citation
SHARP INEQUALITIES FOR THE VARIATION OF THE DISCRETE MAXIMAL FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 1 / February 2017
- Published online by Cambridge University Press:
- 04 November 2016, pp. 94-107
- Print publication:
- February 2017
-
- Article
-
- You have access
- Export citation
Convex Functions on Discrete Time Domains
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 2 / 01 June 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-233
- Print publication:
- 01 June 2016
-
- Article
-
- You have access
- Export citation
QUASI RIESZ TRANSFORMS, HARDY SPACES AND GENERALISED SUB-GAUSSIAN HEAT KERNEL ESTIMATES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 92 / Issue 3 / December 2015
- Published online by Cambridge University Press:
- 10 August 2015, pp. 508-510
- Print publication:
- December 2015
-
- Article
-
- You have access
- Export citation
ASYMPTOTIC INTEGRATION OF SECOND-ORDER NONLINEAR DIFFERENCE EQUATIONS
-
- Journal:
- Glasgow Mathematical Journal / Volume 53 / Issue 2 / May 2011
- Published online by Cambridge University Press:
- 08 December 2010, pp. 223-243
- Print publication:
- May 2011
-
- Article
-
- You have access
- Export citation
YANG–BAXTER MAPS AND THE DISCRETE KP HIERARCHY
-
- Journal:
- Glasgow Mathematical Journal / Volume 51 / Issue A / February 2009
- Published online by Cambridge University Press:
- 01 February 2009, pp. 107-119
- Print publication:
- February 2009
-
- Article
-
- You have access
- Export citation
Hitting Time and Inverse Problems for Markov Chains
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 3 / September 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 640-649
- Print publication:
- September 2008
-
- Article
-
- You have access
- Export citation
REMARKS ON ℓ1 AND
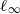 -MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
-MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 84 / Issue 3 / June 2008
- Published online by Cambridge University Press:
- 01 June 2008, pp. 345-365
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
DISCRETE RICCATI EQUATION, HYPERGEOMETRIC FUNCTIONS AND CIRCLE PATTERNS OF SCHRAMM TYPE
-
- Journal:
- Glasgow Mathematical Journal / Volume 47 / Issue A / June 2005
- Published online by Cambridge University Press:
- 14 July 2005, pp. 1-16
- Print publication:
- June 2005
-
- Article
-
- You have access
- Export citation
FORMULAS OF BENDIXSON AND ALEKSEEV FOR DIFFERENCE EQUATIONS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 36 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 23 December 2003, pp. 65-71
- Print publication:
- January 2004
-
- Article
- Export citation
Lp–Lrestimates for the Poisson semigroup on homogeneous trees
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 64 / Issue 1 / February 1998
- Published online by Cambridge University Press:
- 09 April 2009, pp. 20-32
- Print publication:
- February 1998
-
- Article
-
- You have access
- Export citation
Generalized theorem of Hartman-Grobman on measure chains
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 60 / Issue 2 / April 1996
- Published online by Cambridge University Press:
- 09 April 2009, pp. 157-191
- Print publication:
- April 1996
-
- Article
-
- You have access
- Export citation








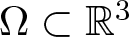
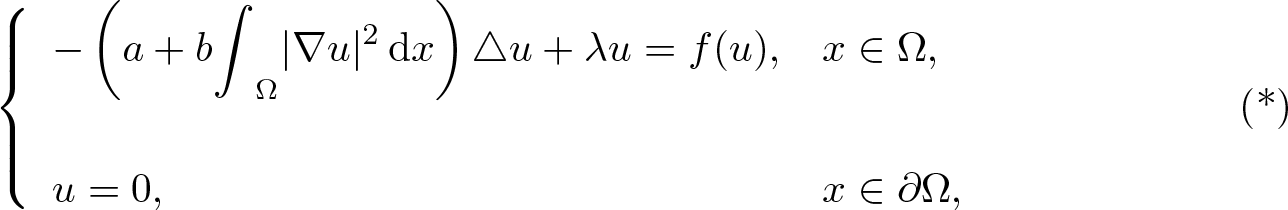
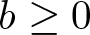
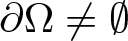
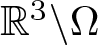
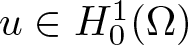
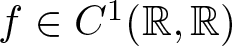
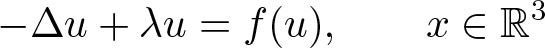
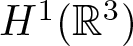
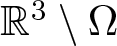
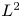
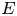
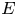
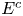
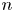
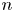
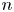
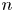
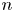
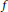

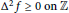
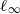 -MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
-MAXIMAL REGULARITY FOR POWER-BOUNDED OPERATORS
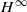 -calculus, and give a complete characterization of this condition in the case of Banach spaces which are
-calculus, and give a complete characterization of this condition in the case of Banach spaces which are  be a homogeneous tree of degree at least three. In this paper we investigate for which values of
be a homogeneous tree of degree at least three. In this paper we investigate for which values of 