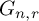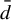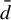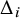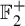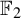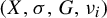Refine search
Actions for selected content:
99 results
KATSURA–EXEL–PARDO SELF-SIMILAR ACTIONS, PUTNAM’S BINARY FACTORS AND THEIR LIMIT SPACES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 31 October 2025, pp. 1-36
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pensive Billiards, Point Vortices, And The Silver Ratio
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 October 2025, e171
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Type invariants for non-abelian odometers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 01 September 2025, pp. 182-210
- Print publication:
- January 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CHARACTERISATION OF DISTAL ACTIONS OF AUTOMORPHISMS ON THE SPACE OF ONE-PARAMETER SUBGROUPS OF LIE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 119 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 15 August 2025, pp. 152-175
- Print publication:
- October 2025
-
- Article
- Export citation
On closure operations in the space of subgroups and applications
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 12 / December 2025
- Published online by Cambridge University Press:
- 05 August 2025, pp. 3728-3748
- Print publication:
- December 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Density properties of orbits for a hypercyclic operator on a Banach space
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 18 July 2025, pp. 1-16
-
- Article
- Export citation
On non-tameness of the Ellis semigroup
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 11 / November 2025
- Published online by Cambridge University Press:
- 30 June 2025, pp. 3419-3429
- Print publication:
- November 2025
-
- Article
- Export citation
Some hyperbolicity revisited and robust transitivity
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 12 / December 2025
- Published online by Cambridge University Press:
- 23 June 2025, pp. 3800-3831
- Print publication:
- December 2025
-
- Article
- Export citation
Joint transitivity for linear iterates
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 February 2025, e34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A variational principle of scaled entropy for amenable group actions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-28
-
- Article
- Export citation
Linear repetitivity beyond abelian groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 1947-1997
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Construction of smooth isomorphic and finite-to-one extensions of irrational rotations which are not almost automorphic
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 1224-1245
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUFFICIENT CONDITIONS FOR A GROUP OF HOMEOMORPHISMS OF THE CANTOR SET TO BE TWO-GENERATED
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 20 September 2024, pp. 2825-2858
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal and proximal examples of
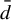 $\bar {d}$-stable and
$\bar {d}$-stable and 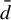 $\bar {d}$-approachable shift spaces
$\bar {d}$-approachable shift spaces
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 10 September 2024, pp. 396-426
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal zero entropy subshifts can be unrestricted along any sparse set
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 2 / February 2025
- Published online by Cambridge University Press:
- 09 September 2024, pp. 566-572
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal subdynamics and minimal flows without characteristic measures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 May 2024, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Similarities and differences between specification and non-uniform specification
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 15 April 2024, pp. 3501-3529
- Print publication:
- December 2024
-
- Article
- Export citation
Substreetutions and more on trees
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 08 April 2024, pp. 2399-2453
- Print publication:
- September 2024
-
- Article
- Export citation
Invariant measures of Toeplitz subshifts on non-amenable groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 11 / November 2024
- Published online by Cambridge University Press:
- 04 March 2024, pp. 3186-3215
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability for hyperbolic groups acting on boundary spheres
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 21 September 2023, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation