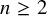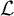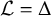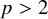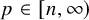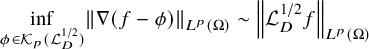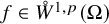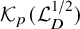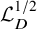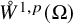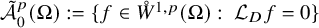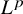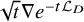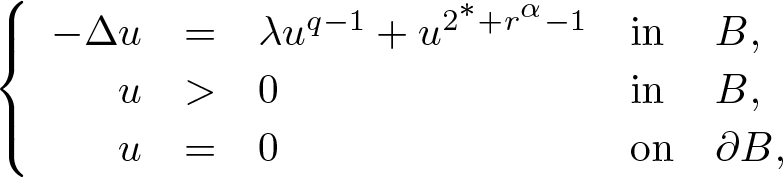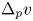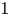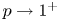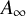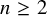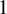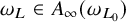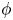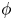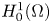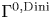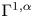Refine search
Actions for selected content:
68 results
Optimization of the principal eigenvalue of the Neumann Laplacian with indefinite weight and monotonicity of minimizers in cylinders
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 15 September 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Pattern formation with jump discontinuity in a predator–prey model with Holling-II functional response
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1-23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Some remarks on Riesz transforms on exterior Lipschitz domains
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 March 2025, e58
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An elliptic operator with a nonlocal term: maximum principle, principal eigenvalue, and applications to a logistic equation with indefinite weight
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 24 February 2025, pp. 1-38
-
- Article
- Export citation
Diffusive convective elliptic problem in variable exponent space and measure data
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 23 January 2025, pp. 1-24
-
- Article
- Export citation
The effect of a perturbation on Brezis-Nirenberg’s problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-16
-
- Article
- Export citation
Prescribing nearly constant curvatures on balls
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 27 October 2023, pp. 756-791
- Print publication:
- June 2025
-
- Article
- Export citation
Groundstates of the planar Schrödinger–Poisson system with potential well and lack of symmetry
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 4 / August 2024
- Published online by Cambridge University Press:
- 22 May 2023, pp. 993-1023
- Print publication:
- August 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Behaviour of solutions to p-Laplacian with Robin boundary conditions as p goes to 1
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 26 January 2023, pp. 105-130
- Print publication:
- February 2024
-
- Article
- Export citation
On the
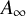 $A_{\infty }$ condition for elliptic operators in 1-sided nontangentially accessible domains satisfying the capacity density condition
$A_{\infty }$ condition for elliptic operators in 1-sided nontangentially accessible domains satisfying the capacity density condition
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 05 August 2022, e59
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Steady state diffusion in tubular structures: Assessment of one-dimensional models
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 34 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 25 April 2022, pp. 262-279
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Optimal Hardy-weights for the (p, A)-Laplacian with a potential term
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 153 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 17 December 2021, pp. 289-306
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Existence results for a nonlinear nonautonomous transmission problem via domain perturbation
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 11 October 2021, pp. 1451-1476
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Positive solutions for a degenerate Kirchhoff problem
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 3 / August 2021
- Published online by Cambridge University Press:
- 19 August 2021, pp. 675-688
-
- Article
- Export citation
Existence of solution for elliptic equations with supercritical Trudinger–Moser growth
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 16 February 2021, pp. 291-310
- Print publication:
- April 2022
-
- Article
- Export citation
Borderline gradient estimates at the boundary in Carnot groups
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 6 / December 2021
- Published online by Cambridge University Press:
- 02 December 2020, pp. 1920-1953
- Print publication:
- December 2021
-
- Article
- Export citation
On supercritical problems involving the Laplace operator
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 1 / February 2021
- Published online by Cambridge University Press:
- 27 February 2020, pp. 187-201
- Print publication:
- February 2021
-
- Article
- Export citation
Gradient estimates for the constant mean curvature equation in hyperbolic space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 09 December 2019, pp. 3216-3230
- Print publication:
- December 2020
-
- Article
- Export citation
On the boundary regularity of phase-fields for Willmore's energy
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 1017-1035
- Print publication:
- August 2019
-
- Article
- Export citation
On the avascular ellipsoidal tumour growth model within a nutritive environment
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 31 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 18 September 2018, pp. 111-142
-
- Article
- Export citation