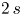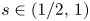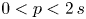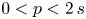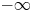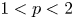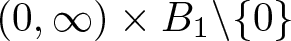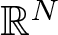Refine search
Actions for selected content:
19 results
Blow-up of cylindrically symmetric solutions for fractional NLS
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 08 September 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global existence and some qualitative properties of weak solutions for a class of pseudo-parabolic equations with a logarithmic nonlinearity in whole
 $\mathbb{R}^{N}$
$\mathbb{R}^{N}$
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 01 August 2025, pp. 1-44
-
- Article
- Export citation
Concentration and oscillation analysis of positive solutions to semilinear elliptic equations with exponential growth in a disc. II
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 31 July 2025, pp. 1-28
-
- Article
- Export citation
Global dynamics for the generalised chemotaxis-Navier–Stokes system in
 $\mathbb{R}^3$
$\mathbb{R}^3$
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 22 April 2025, pp. 1-38
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On blow-up for the supercritical defocusing nonlinear wave equation
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 31 March 2025, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A critical non-homogeneous heat equation with weighted source
- Part of
-
- Journal:
- European Journal of Applied Mathematics , First View
- Published online by Cambridge University Press:
- 06 March 2025, pp. 1-12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic estimate of solutions in a 4th-order parabolic equation with the Frobenius norm of a Hessian matrix
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 91-108
- Print publication:
- March 2025
-
- Article
- Export citation
Blowup of cylindrically symmetric solutions for biharmonic NLS
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 03 October 2024, pp. 1085-1098
-
- Article
- Export citation
Unbounded Sturm attractors for quasilinear parabolic equations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 08 March 2024, pp. 542-565
-
- Article
- Export citation
On large solutions for fractional Hamilton–Jacobi equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 11 July 2023, pp. 1313-1335
- Print publication:
- October 2024
-
- Article
- Export citation
Higher-order evolution inequalities involving convection and Hardy-Leray potential terms in a bounded domain
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 05 May 2023, pp. 366-390
-
- Article
- Export citation
Convergence for the fractional p-Laplacian and its application to the extended Nirenberg problem
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 05 April 2023, pp. 660-672
- Print publication:
- April 2024
-
- Article
- Export citation
Does indirectness of signal production reduce the explosion-supporting potential in chemotaxis–haptotaxis systems? Global classical solvability in a class of models for cancer invasion (and more)
- Part of
-
- Journal:
- European Journal of Applied Mathematics / Volume 32 / Issue 4 / August 2021
- Published online by Cambridge University Press:
- 17 July 2020, pp. 618-651
-
- Article
- Export citation
Existence, non-existence and blow-up behaviour of minimizers for the mass-critical fractional non-linear Schrödinger equations with periodic potentials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 6 / December 2020
- Published online by Cambridge University Press:
- 13 January 2020, pp. 3252-3292
- Print publication:
- December 2020
-
- Article
- Export citation
Autonomous and non-autonomous unbounded attractors under perturbations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 4 / August 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 877-903
- Print publication:
- August 2019
-
- Article
- Export citation
Prescribed mean curvature equation on the unit ball in the presence of reflection or rotation symmetry
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 3 / June 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 781-794
- Print publication:
- June 2019
-
- Article
- Export citation
A mean field equation involving positively supported probability measures: blow-up phenomena and variational aspects
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 149 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 27 December 2018, pp. 325-352
- Print publication:
- April 2019
-
- Article
- Export citation
EXISTENCE AND BLOW-UP OF SOLUTIONS TO A PARABOLIC EQUATION WITH NONSTANDARD GROWTH CONDITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 99 / Issue 2 / April 2019
- Published online by Cambridge University Press:
- 11 December 2018, pp. 242-249
- Print publication:
- April 2019
-
- Article
-
- You have access
- Export citation
A Class of Fourth Order Damped Wave Equations with Arbitrary Positive Initial Energy
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 14 September 2018, pp. 165-178
-
- Article
- Export citation