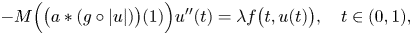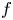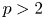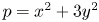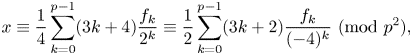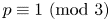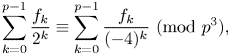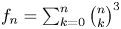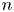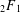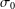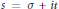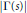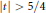Refine search
Actions for selected content:
10 results
A unified topological analysis of variable growth Kirchhoff-type equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 09 September 2025, pp. 1-30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A unified characterization of convolution coefficients in nonlocal differential equations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 18 September 2024, pp. 1-19
-
- Article
- Export citation
On two congruence conjectures of Z.-W. Sun involving Franel numbers
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 16 May 2023, pp. 887-905
- Print publication:
- June 2024
-
- Article
- Export citation
On the distribution of the digits of quotients of integers and primes
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 279-295
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SUPERCONGRUENCES INVOLVING
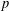 $p$ -ADIC GAMMA FUNCTIONS
$p$ -ADIC GAMMA FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 98 / Issue 1 / August 2018
- Published online by Cambridge University Press:
- 30 May 2018, pp. 27-37
- Print publication:
- August 2018
-
- Article
-
- You have access
- Export citation
ON ALGEBRAIC DIFFERENTIAL EQUATIONS FOR THE GAMMA FUNCTION AND
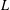 $L$ -FUNCTIONS IN THE EXTENDED SELBERG CLASS
$L$ -FUNCTIONS IN THE EXTENDED SELBERG CLASS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 1 / August 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 36-43
- Print publication:
- August 2017
-
- Article
-
- You have access
- Export citation
COMPLETE MONOTONICITY OF A FUNCTION INVOLVING THE DIVIDED DIFFERENCE OF PSI FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 18 January 2013, pp. 309-319
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
On the Horizontal Monotonicity of |Γ(s)|
-
- Journal:
- Canadian Mathematical Bulletin / Volume 54 / Issue 3 / 01 September 2011
- Published online by Cambridge University Press:
- 20 November 2018, pp. 538-543
- Print publication:
- 01 September 2011
-
- Article
-
- You have access
- Export citation
Laplace Transforms of Probability Distributions and Their Inversions are Easy on Logarithmic Scales
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 45 / Issue 2 / June 2008
- Published online by Cambridge University Press:
- 14 July 2016, pp. 531-541
- Print publication:
- June 2008
-
- Article
-
- You have access
- Export citation
On modification of the q-L-series and its applications
-
- Journal:
- Nagoya Mathematical Journal / Volume 164 / December 2001
- Published online by Cambridge University Press:
- 22 January 2016, pp. 185-197
- Print publication:
- December 2001
-
- Article
-
- You have access
- Export citation