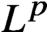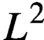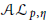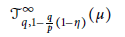Refine search
Actions for selected content:
3 results
Hilbert matrix operator acting between conformally invariant spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 12 December 2024, pp. 550-567
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Global boundedness of a class of multilinear Fourier integral operators
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 22 February 2021, e14
-
- Article
-
- You have access
- Open access
- Export citation
The Carleson Measure Problem Between Analytic Morrey Spaces
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 4 / 01 December 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 878-890
- Print publication:
- 01 December 2016
-
- Article
-
- You have access
- Export citation