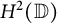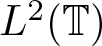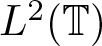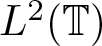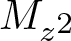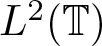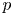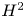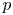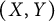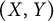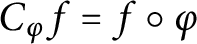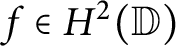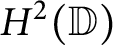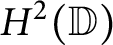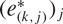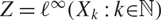Refine search
Actions for selected content:
30 results
Isometric dilation and Sarason’s commutant lifting theorem in several variables
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 25 February 2025, pp. 1-33
-
- Article
- Export citation
Cyclicity of the shift operator through Bezout identities
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 28 January 2025, pp. 684-708
- Print publication:
- September 2025
-
- Article
- Export citation
Nearly invariant Brangesian subspaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 07 January 2025, pp. 318-337
- Print publication:
- March 2025
-
- Article
- Export citation
Hilbert matrix operator acting between conformally invariant spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 12 December 2024, pp. 550-567
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Phase retrieval on circles and lines
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 10 May 2024, pp. 927-935
- Print publication:
- December 2024
-
- Article
- Export citation
Inhomogeneous Poisson processes in the disk and interpolation
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 3 / August 2024
- Published online by Cambridge University Press:
- 30 April 2024, pp. 749-777
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Integral mean estimates for univalent and locally univalent harmonic mappings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 15 January 2024, pp. 655-669
- Print publication:
- September 2024
-
- Article
- Export citation
Commutants and complex symmetry of finite Blaschke product multiplication operator in
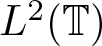 $L^2(\mathbb{T})$
$L^2(\mathbb{T})$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 11 January 2024, pp. 261-286
-
- Article
- Export citation
Symmetric and antisymmetric tensor products for the function-theoretic operator theorist
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 22 December 2023, pp. 324-346
- Print publication:
- February 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Sub-Bergman Hilbert spaces on the unit disk III
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 22 August 2023, pp. 1520-1537
- Print publication:
- October 2024
-
- Article
- Export citation
Schatten class composition operators on the Hardy space
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 154 / Issue 5 / October 2024
- Published online by Cambridge University Press:
- 24 July 2023, pp. 1364-1377
- Print publication:
- October 2024
-
- Article
- Export citation
General Toeplitz kernels and
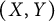 $(X,Y)$-invariance
$(X,Y)$-invariance
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 March 2023, pp. 680-706
- Print publication:
- April 2024
-
- Article
- Export citation
Polynomial null solutions to bosonic Laplacians, bosonic Bergman and Hardy spaces
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 13 October 2022, pp. 958-989
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Model spaces invariant under composition operators
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 25 March 2022, pp. 204-217
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FUNCTIONAL CALCULI FOR SECTORIAL OPERATORS AND RELATED FUNCTION THEORY
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 3 / May 2023
- Published online by Cambridge University Press:
- 04 October 2021, pp. 1383-1463
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CARLESON INTERPOLATING SEQUENCES FOR BANACH SPACES OF ANALYTIC FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 6 / November 2022
- Published online by Cambridge University Press:
- 29 March 2021, pp. 1915-1945
- Print publication:
- November 2022
-
- Article
- Export citation
Global boundedness of a class of multilinear Fourier integral operators
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 9 / 2021
- Published online by Cambridge University Press:
- 22 February 2021, e14
-
- Article
-
- You have access
- Open access
- Export citation
The factorisation property of l∞(Xk)
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 171 / Issue 2 / September 2021
- Published online by Cambridge University Press:
- 10 December 2020, pp. 421-448
- Print publication:
- September 2021
-
- Article
-
- You have access
- Open access
- Export citation
A note on the phase retrieval of holomorphic functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 4 / December 2021
- Published online by Cambridge University Press:
- 08 October 2020, pp. 779-786
- Print publication:
- December 2021
-
- Article
- Export citation
Derivatives of Blaschke Products and Model Space Functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 12 November 2019, pp. 716-725
- Print publication:
- December 2020
-
- Article
- Export citation