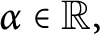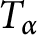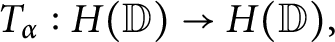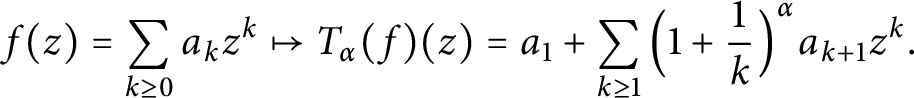Refine search
Actions for selected content:
6 results
RADIAL ASYMPTOTICS OF GENERATING FUNCTIONS OF k-REGULAR SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 3 / December 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 528-534
- Print publication:
- December 2024
-
- Article
- Export citation
Growth of frequently hypercyclic functions for some weighted Taylor shifts on the unit disc
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 11 June 2020, pp. 264-281
- Print publication:
- June 2021
-
- Article
- Export citation
TRANSCENDENCE OVER MEROMORPHIC FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 95 / Issue 3 / June 2017
- Published online by Cambridge University Press:
- 13 March 2017, pp. 393-399
- Print publication:
- June 2017
-
- Article
-
- You have access
- Export citation
INFINITE PRODUCTS OF CYCLOTOMIC POLYNOMIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 91 / Issue 3 / June 2015
- Published online by Cambridge University Press:
- 26 February 2015, pp. 400-411
- Print publication:
- June 2015
-
- Article
-
- You have access
- Export citation
Exceptional Sets in Hartogs Domains
-
- Journal:
- Canadian Mathematical Bulletin / Volume 48 / Issue 4 / 01 December 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 580-586
- Print publication:
- 01 December 2005
-
- Article
-
- You have access
- Export citation
UNIVERSAL TAYLOR SERIES ON GENERAL DOUBLY CONNECTED DOMAINS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 37 / Issue 6 / December 2005
- Published online by Cambridge University Press:
- 12 December 2005, pp. 878-884
- Print publication:
- December 2005
-
- Article
- Export citation