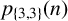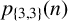Refine search
Actions for selected content:
2 results
PROOF OF SOME CONJECTURAL CONGRUENCES OF DA SILVA AND SELLERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 13 December 2021, pp. 57-61
- Print publication:
- August 2022
-
- Article
- Export citation
-
Let
$p_{\{3, 3\}}(n)$ denote the number of 
$3$-regular partitions in three colours. Da Silva and Sellers [‘Arithmetic properties of 3-regular partitions in three colours’, Bull. Aust. Math. Soc. 104(3) (2021), 415–423] conjectured four Ramanujan-like congruences modulo 
$5$ satisfied by 
$p_{\{3, 3\}}(n)$. We confirm these conjectural congruences using the theory of modular forms.
ARITHMETIC PROPERTIES OF 3-REGULAR PARTITIONS IN THREE COLOURS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 07 June 2021, pp. 415-423
- Print publication:
- December 2021
-
- Article
- Export citation
-
Gireesh and Mahadeva Naika [‘On 3-regular partitions in 3-colors’, Indian J. Pure Appl. Math. 50 (2019), 137–148] proved an infinite family of congruences modulo powers of 3 for the function
$p_{\{3,3\}}(n)$, the number of 3-regular partitions in three colours. In this paper, using elementary generating function manipulations and classical techniques, we significantly extend the list of proven arithmetic properties satisfied by 
$p_{\{3,3\}}(n).$
