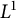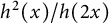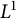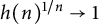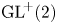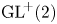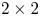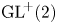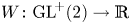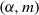Refine search
Actions for selected content:
13 results
On some convexity questions of Handelman
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 16 May 2024, pp. 936-939
- Print publication:
- December 2024
-
- Article
- Export citation
A rank-one convex, nonpolyconvex isotropic function on
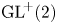 $\textrm {GL}^{\!+}(2)$ with compact connected sublevel sets
$\textrm {GL}^{\!+}(2)$ with compact connected sublevel sets
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 02 February 2022, pp. 356-381
- Print publication:
- April 2022
-
- Article
- Export citation
INEQUALITIES FOR DRAGOMIR’S MAPPINGS VIA STIELTJES INTEGRALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 16 January 2020, pp. 240-250
- Print publication:
- October 2020
-
- Article
-
- You have access
- Export citation
Quasiconvex relaxation of isotropic functions in incompressible planar hyperelasticity
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 5 / October 2020
- Published online by Cambridge University Press:
- 11 June 2019, pp. 2620-2631
- Print publication:
- October 2020
-
- Article
-
- You have access
- Open access
- Export citation
THE TWO-TRAIN SEPARATION PROBLEM ON LEVEL TRACK WITH DISCRETE CONTROL
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 60 / Issue 2 / October 2018
- Published online by Cambridge University Press:
- 29 October 2018, pp. 137-174
-
- Article
-
- You have access
- Export citation
THE COST–TIME CURVE FOR AN OPTIMAL TRAIN JOURNEY ON LEVEL TRACK
- Part of
-
- Journal:
- The ANZIAM Journal / Volume 58 / Issue 1 / July 2016
- Published online by Cambridge University Press:
- 01 July 2016, pp. 10-32
-
- Article
-
- You have access
- Export citation
GENERALISATIONS OF INTEGRAL INEQUALITIES OF HERMITE–HADAMARD TYPE THROUGH CONVEXITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 88 / Issue 2 / October 2013
- Published online by Cambridge University Press:
- 20 December 2012, pp. 320-330
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
ON APPROXIMATELY MIDCONVEX FUNCTIONS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 36 / Issue 3 / May 2004
- Published online by Cambridge University Press:
- 28 April 2004, pp. 339-350
- Print publication:
- May 2004
-
- Article
- Export citation
On Ψ direct sums of Banach spaces and convexity
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 75 / Issue 3 / December 2003
- Published online by Cambridge University Press:
- 09 April 2009, pp. 413-422
- Print publication:
- December 2003
-
- Article
-
- You have access
- Export citation
Convexité, complête monotonie et inégalités sur les fonctions zêta et gamma, sur les fonctions des opérateurs de Baskakov et sur des fonctions arithmétiques
-
- Journal:
- Canadian Journal of Mathematics / Volume 54 / Issue 5 / 01 October 2002
- Published online by Cambridge University Press:
- 20 November 2018, pp. 916-944
- Print publication:
- 01 October 2002
-
- Article
-
- You have access
- Export citation
Concavity and reflected Lévy processes
- Part of
-
- Journal:
- Journal of Applied Probability / Volume 29 / Issue 1 / March 1992
- Published online by Cambridge University Press:
- 14 July 2016, pp. 209-215
- Print publication:
- March 1992
-
- Article
- Export citation
The Exceptional Sets in the Definition of the Pn -Integral
-
- Journal:
- Canadian Mathematical Bulletin / Volume 25 / Issue 4 / 01 December 1982
- Published online by Cambridge University Press:
- 20 November 2018, pp. 385-391
- Print publication:
- 01 December 1982
-
- Article
-
- You have access
- Export citation
Splicing n-Convex Functions using Splines
-
- Journal:
- Canadian Mathematical Bulletin / Volume 23 / Issue 1 / 01 March 1980
- Published online by Cambridge University Press:
- 20 November 2018, pp. 107-109
- Print publication:
- 01 March 1980
-
- Article
-
- You have access
- Export citation