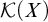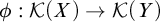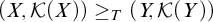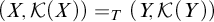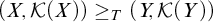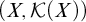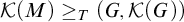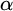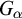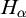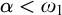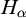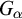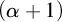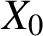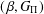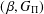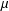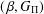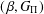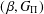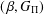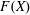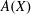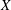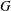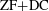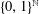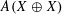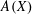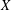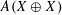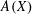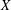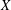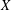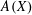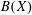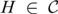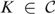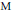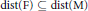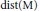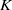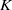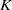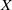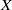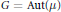Refine search
Actions for selected content:
25 results
ON EQUIVALENCE RELATIONS INDUCED BY POLISH GROUPS ADMITTING COMPATIBLE TWO-SIDED INVARIANT METRICS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 03 February 2025, pp. 1-38
-
- Article
- Export citation
THE SHAPE OF COMPACT COVERS
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 29 October 2024, pp. 1-15
-
- Article
- Export citation
A HIERARCHY ON NON-ARCHIMEDEAN POLISH GROUPS ADMITTING A COMPATIBLE COMPLETE LEFT-INVARIANT METRIC
- Part of
-
- Journal:
- The Journal of Symbolic Logic , First View
- Published online by Cambridge University Press:
- 06 February 2024, pp. 1-19
-
- Article
- Export citation
A TOPOMETRIC EFFROS THEOREM
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 90 / Issue 1 / March 2025
- Published online by Cambridge University Press:
- 02 February 2023, pp. 310-320
- Print publication:
- March 2025
-
- Article
- Export citation
Invariant Ideal Axiom
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 20 May 2022, e29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Chief factors in Polish groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 30 June 2021, pp. 239-296
- Print publication:
- September 2022
-
- Article
- Export citation
ON GRAEV’S THEOREM FOR FREE PRODUCTS OF HAUSDORFF TOPOLOGICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 29 March 2021, pp. 475-483
- Print publication:
- December 2021
-
- Article
- Export citation
ON
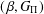 $(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-UNFAVOURABLE SPACES
$(\,\unicode[STIX]{x1D6FD},G_{\unicode[STIX]{x1D6F1}})$-UNFAVOURABLE SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 3 / December 2020
- Published online by Cambridge University Press:
- 16 March 2020, pp. 439-450
- Print publication:
- December 2020
-
- Article
-
- You have access
- Export citation
FINITENESS OF TOPOLOGICAL ENTROPY FOR LOCALLY COMPACT ABELIAN GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 26 February 2020, pp. 81-105
- Print publication:
- January 2021
-
- Article
- Export citation
Separable Quotients of Free Topological Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 3 / September 2020
- Published online by Cambridge University Press:
- 29 November 2019, pp. 610-623
- Print publication:
- September 2020
-
- Article
-
- You have access
- Export citation
CONTINUITY OF UNIVERSALLY MEASURABLE HOMOMORPHISMS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 7 / 2019
- Published online by Cambridge University Press:
- 13 August 2019, e5
-
- Article
-
- You have access
- Open access
- Export citation
Completeness of Infinite-dimensional Lie Groups in Their Left Uniformity
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 1 / February 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 131-152
- Print publication:
- February 2019
-
- Article
-
- You have access
- Open access
- Export citation
EMBEDDING OF THE FREE ABELIAN TOPOLOGICAL GROUP
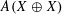 $A(X\oplus X)$ INTO
$A(X\oplus X)$ INTO 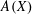 $A(X)$
$A(X)$
- Part of
-
- Journal:
- Mathematika / Volume 65 / Issue 3 / 2019
- Published online by Cambridge University Press:
- 17 April 2019, pp. 708-718
- Print publication:
- 2019
-
- Article
- Export citation
AUTOMORPHISM GROUPS OF RANDOMIZED STRUCTURES
-
- Journal:
- The Journal of Symbolic Logic / Volume 82 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 08 September 2017, pp. 1150-1179
- Print publication:
- September 2017
-
- Article
- Export citation
GREY SUBSETS OF POLISH SPACES
-
- Journal:
- The Journal of Symbolic Logic / Volume 80 / Issue 4 / December 2015
- Published online by Cambridge University Press:
- 22 December 2015, pp. 1379-1397
- Print publication:
- December 2015
-
- Article
- Export citation
UNIVERSAL SUBGROUPS OF POLISH GROUPS
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 4 / December 2014
- Published online by Cambridge University Press:
- 12 December 2014, pp. 1148-1183
- Print publication:
- December 2014
-
- Article
- Export citation
Distance Sets of Urysohn Metric Spaces
-
- Journal:
- Canadian Journal of Mathematics / Volume 65 / Issue 1 / 01 February 2013
- Published online by Cambridge University Press:
- 20 November 2018, pp. 222-240
- Print publication:
- 01 February 2013
-
- Article
-
- You have access
- Export citation
NOTES ON
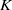 $K$-TOPOLOGICAL GROUPS AND HOMEOMORPHISMS OF TOPOLOGICAL GROUPS
$K$-TOPOLOGICAL GROUPS AND HOMEOMORPHISMS OF TOPOLOGICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 87 / Issue 3 / June 2013
- Published online by Cambridge University Press:
- 30 August 2012, pp. 493-502
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
The Group Aut (μ) is Roelcke Precompact
-
- Journal:
- Canadian Mathematical Bulletin / Volume 55 / Issue 2 / 01 June 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 297-302
- Print publication:
- 01 June 2012
-
- Article
-
- You have access
- Export citation
VARIETIES OF ABELIAN TOPOLOGICAL GROUPS AND SCATTERED SPACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 78 / Issue 3 / December 2008
- Published online by Cambridge University Press:
- 01 December 2008, pp. 487-495
- Print publication:
- December 2008
-
- Article
-
- You have access
- Export citation