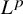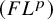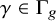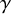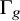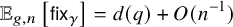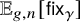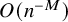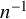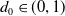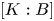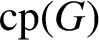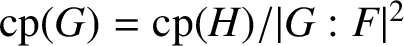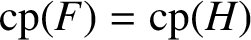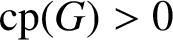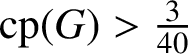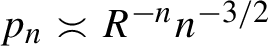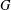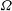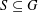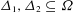Refine search
Actions for selected content:
31 results
Uniform models and short curves for random 3-manifolds
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 3 / March 2025
- Published online by Cambridge University Press:
- 27 June 2025, pp. 447-502
- Print publication:
- March 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Base sizes of primitive groups of diagonal type
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 04 January 2024, e2
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a variant of the product replacement algorithm
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 09 January 2024, pp. 221-228
- Print publication:
- January 2024
-
- Article
- Export citation
Żuk’s criterion for Banach spaces and random groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 12 September 2023, e79
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Asymptotic Statistics of Random Covering Surfaces
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 15 May 2023, e15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Products of derangements in simple permutation groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 23 September 2022, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Property (T) in k-gonal random groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 22 February 2022, pp. 734-738
- Print publication:
- September 2022
-
- Article
- Export citation
On the commuting probability for subgroups of a finite group
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 6 / December 2022
- Published online by Cambridge University Press:
- 18 November 2021, pp. 1551-1564
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Compact groups with a set of positive Haar measure satisfying a nilpotent law
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 2 / September 2022
- Published online by Cambridge University Press:
- 19 July 2021, pp. 329-332
- Print publication:
- September 2022
-
- Article
- Export citation
COMMUTING PROBABILITY OF COMPACT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 24 June 2021, pp. 87-91
- Print publication:
- February 2022
-
- Article
- Export citation
COMMUTATOR EQUATIONS IN FINITE GROUPS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 03 June 2021, pp. 320-335
- Print publication:
- May 2022
-
- Article
- Export citation
Local limit theorems in relatively hyperbolic groups I: rough estimates
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 6 / June 2022
- Published online by Cambridge University Press:
- 23 March 2021, pp. 1926-1966
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- Export citation
CHARACTER LEVELS AND CHARACTER BOUNDS
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 8 / 2020
- Published online by Cambridge University Press:
- 24 January 2020, e2
-
- Article
-
- You have access
- Open access
- Export citation
BOREL DENSITY FOR APPROXIMATE LATTICES
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 7 / 2019
- Published online by Cambridge University Press:
- 05 November 2019, e40
-
- Article
-
- You have access
- Open access
- Export citation
Corrigendum to ‘Mixing, Communication Complexity and Conjectures of Gowers and Viola’
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 6 / November 2017
- Published online by Cambridge University Press:
- 01 August 2017, pp. 954-955
-
- Article
-
- You have access
- Export citation
QUASIRANDOM GROUP ACTIONS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 4 / 2016
- Published online by Cambridge University Press:
- 30 August 2016, e24
-
- Article
-
- You have access
- Open access
- Export citation
Mixing, Communication Complexity and Conjectures of Gowers and Viola
-
- Journal:
- Combinatorics, Probability and Computing / Volume 26 / Issue 4 / July 2017
- Published online by Cambridge University Press:
- 07 June 2016, pp. 628-640
-
- Article
- Export citation
THE SUBGROUP COMMUTATIVITY DEGREE OF FINITE
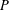 $P$-GROUPS
$P$-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 93 / Issue 1 / February 2016
- Published online by Cambridge University Press:
- 08 July 2015, pp. 37-41
- Print publication:
- February 2016
-
- Article
-
- You have access
- Export citation
Virtual geometricity is rare
- Part of
-
- Journal:
- LMS Journal of Computation and Mathematics / Volume 18 / Issue 1 / 2015
- Published online by Cambridge University Press:
- 01 July 2015, pp. 444-455
-
- Article
-
- You have access
- Export citation
QUASI-RANDOM PROFINITE GROUPS
-
- Journal:
- Glasgow Mathematical Journal / Volume 57 / Issue 1 / January 2015
- Published online by Cambridge University Press:
- 22 December 2014, pp. 181-200
- Print publication:
- January 2015
-
- Article
-
- You have access
- Export citation