Refine search
Actions for selected content:
6 results
Type invariants for non-abelian odometers
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-29
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Abelian groups from random hypergraphs
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 32 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 654-664
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE GENERATING GRAPH OF INFINITE ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 68-75
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
CHARACTERIZING AUTOMORPHISM GROUPS OF ORDERED ABELIAN GROUPS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 3 / May 2003
- Published online by Cambridge University Press:
- 12 May 2003, pp. 289-292
- Print publication:
- May 2003
-
- Article
- Export citation
On Finite Essential Extensions of Torsion Free Abelian Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 48 / Issue 5 / 01 October 1996
- Published online by Cambridge University Press:
- 20 November 2018, pp. 918-929
- Print publication:
- 01 October 1996
-
- Article
-
- You have access
- Export citation
On p-Large Subgroups of p-Torsion Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 27 / Issue 4 / 01 December 1984
- Published online by Cambridge University Press:
- 20 November 2018, pp. 410-416
- Print publication:
- 01 December 1984
-
- Article
-
- You have access
- Export citation
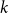
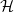
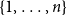
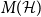
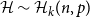
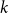
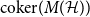
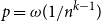
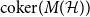
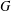
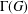
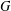
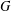
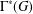
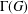
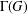
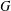
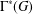
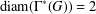
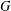
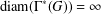
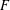
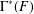
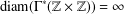
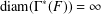
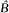 , le complété
, le complété 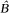 engendrés par un élément.
engendrés par un élément.