We show how finiteness properties of a group and a subgroup transfer to finiteness properties of the Schlichting completion relative to this subgroup.n Further, we provide a criterion when the dense embedding of a discrete group into the Schlichting completion relative to one of its subgroups induces an isomorphism in (continuous) cohomology. As an application, we show that the continuous cohomology of the Neretin group vanishes in all positive degrees.

In this paper, we study triple-product-free sets, which are analogous to the widely studied concept of product-free sets. A nonempty subset S of a group G is triple-product-free if $abc \notin S$ for all $a, b, c \in S$. If S is triple-product-free and is not a proper subset of any other triple-product-free set, we say that S is locally maximal. We classify all groups containing a locally maximal triple-product-free set of size 1. We then derive necessary and sufficient conditions for a subset of a group to be locally maximal triple-product-free, and conclude with some observations and comparisons with the situation for standard product-free sets.

We improve a recent construction of Andrés Navas to produce the first examples of $C^2$-undistorted diffeomorphisms of the interval that are $C^{1+\alpha }$-distorted (for every ${\alpha < 1}$). We do this via explicit computations due to the failure of an extension to class $C^{1+\alpha }$ of a classical lemma related to the work of Nancy Kopell.

As a special case of fully invariant subgroups, strongly invariant subgroups are introduced and studied for Abelian groups.

An epimorphism $\phi :\,G\,\to \,H$ of groups, where $G$ has rank $n$ , is called coessential if every (ordered) generating $n$ -tuple of $H$ can be lifted along $\phi $ to a generating $n$ -tuple for $G$ . We discuss this property in the context of the category of groups, and establish a criterion for such a group $G$ to have the property that its abelianization epimorphism $G\,\to \,{G}/{[G,G]}\;$ , where $[G,\,G]$ is the commutator subgroup, is coessential. We give an example of a family of 2-generator groups whose abelianization epimorphism is not coessential. This family also provides counterexamples to the generalized Andrews–Curtis conjecture.

In this note, we give a homology-free proof that the non-abelian tensor product of two finite groups is finite. In addition, we provide an explicit proof that the non-abelian tensor product of two finite p-groups is a finite p-group.

We show that if G is a group and A⊂G is a finite set with ∣A2∣≤K∣A∣, then there is a symmetric neighbourhood of the identity S such that Sk⊂A2A−2 and ∣S∣≥exp (−KO(k))∣A∣.

Using ideas of S. Wassermann on non-exact ${{C}^{*}}$ -algebras and property $\text{T}$ groups, we show that one of his examples of non-invertible ${{C}^{*}}$ -extensions is not semi-invertible. To prove this, we show that a certain element vanishes in the asymptotic tensor product. We also show that a modification of the example gives a ${{C}^{*}}$ -extension which is not even invertible up to homotopy.

Tensor analogues of right 2-Engel elements in groups were introduced by D. P. Biddle and L.-C. Kappe. We investigate the properties of right 2-Engel tensor elements and introduce the concept of $2_{\otimes}$-Engel margin. With the help of these results we describe the structure of $2_{\otimes}$-Engel groups. In particular, we prove a tensor version of Levi's theorem for 2-Engel groups and determine tensor squares of two-generator $2_{\otimes}$-Engel $p$-groups.

The tensor center of a group $G$ is the set of elements $a$ in $G$ such that $a\otimes g = 1_\otimes$ for all $g$ in $G$. It is a characteristic subgroup of $G$ contained in its center. We introduce tensor analogues of various other subgroups of a group such as centralizers and 2-Engel elements and investigate their embedding in the group as well as interrelationships between those subgroups.

Let $\phi\,{:}\,G \to G$ be a group endomorphism where G is a finitely generated group of exponential growth, and denote by $R(\phi)$ the number of twisted ϕ-conjugacy classes. Fel'shtyn and Hill (K-theory 8 (1994) 367–393) conjectured that if ϕ is injective, then R(ϕ) is infinite. This paper shows that this conjecture does not hold in general. In fact, R(ϕ) can be finite for some automorphism ϕ. Furthermore, for a certain family of polycyclic groups, there is no injective endomorphism ϕ with $R({\phi}^n)\,{<}\,\infty$ for all n.

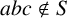
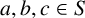
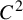
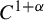
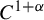
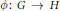
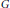
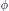
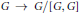
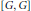
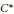
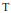
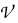For any variety of groups, the relative inner rank of a given groupG is defined to be the maximal rank of the -free homomorphic images of G. In this paper we explore metabelian inner ranks of certain one-relator groups. Using the well-known Quillen-Suslin Theorem, in conjunction with an elegant result of Artamonov, we prove that if r is any "Δ-modular" element of the free metabelian group Mn of rank n > 2 then the metabelian inner rank of the quotient group Mn/(r) is at most [n/2]. As a corollary we deduce that the metabelian inner rank of the (orientable) surface group of genus k is precisely k. This extends the corresponding result of Zieschang about the absolute inner ranks of these surface groups. In continuation of some further applications of the Quillen-Suslin Theorem we give necessary and sufficient conditions for a system g = (g1,..., gk) of k elements of a free metabelian group Mn, k ≤ n, to be a part of a basis of Mn. This extends results of Bachmuth and Timoshenko who considered the cases k = n and k < n — 3 respectively.

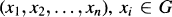Let G be a group and n(≧ 2) an integer. We say that G belongs to the class of groups P n if every product of n elements can be reordered, i.e. for all n-tuples , there exists a non-trivial element σ in the symmetric group Σn such that Let P denote the union of the classes P n , n ≧ 2. Clearly every finite group belongs to P and each class P n is closed with respect to forming subgroups and factor groups.