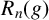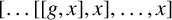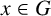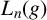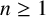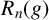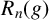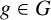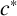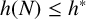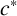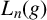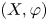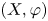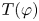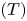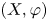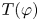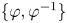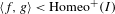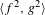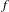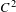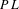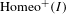Refine search
Actions for selected content:
17 results
Ordered bases, order-preserving automorphisms and bi-orderable link groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 02 October 2025, pp. 1-17
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
RIGHT ENGEL CONDITIONS FOR ORDERABLE GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 27 June 2025, pp. 1-7
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generalized torsion orders and Alexander polynomials
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 08 January 2025, pp. 401-420
- Print publication:
- June 2025
-
- Article
- Export citation
Order-automorphism groups of Archimedean ordered groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 23 December 2024, pp. 628-633
- Print publication:
- June 2025
-
- Article
- Export citation
Cyclic orders and graphs of groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 21 October 2024, pp. 1125-1136
-
- Article
- Export citation
COMPUTABILITY, ORDERS, AND SOLVABLE GROUPS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 4 / December 2020
- Published online by Cambridge University Press:
- 22 October 2020, pp. 1588-1598
- Print publication:
- December 2020
-
- Article
- Export citation
Groups of piecewise linear homeomorphisms of flows
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 05 October 2020, pp. 1595-1622
- Print publication:
- August 2020
-
- Article
- Export citation
Orders on Trees and Free Products of Left-ordered Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 31 March 2020, pp. 335-347
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
2-chains and square roots of Thompson’s group
 $F$
$F$
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 40 / Issue 9 / September 2020
- Published online by Cambridge University Press:
- 25 March 2019, pp. 2515-2532
- Print publication:
- September 2020
-
- Article
- Export citation
ON THE STRUCTURE OF GROUPS ENDOWED WITH A COMPATIBLE C-RELATION
-
- Journal:
- The Journal of Symbolic Logic / Volume 83 / Issue 3 / September 2018
- Published online by Cambridge University Press:
- 23 October 2018, pp. 939-966
- Print publication:
- September 2018
-
- Article
- Export citation
Non-Right-Orderable 3-Manifold Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 53 / Issue 4 / 01 December 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 706-718
- Print publication:
- 01 December 2010
-
- Article
-
- You have access
- Export citation
Non-Left-Orderable 3-Manifold Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 48 / Issue 1 / 01 March 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 32-40
- Print publication:
- 01 March 2005
-
- Article
-
- You have access
- Export citation
EMBEDDING FINITELY GENERATED ABELIAN LATTICE-ORDERED GROUPS: HIGMAN'S THEOREM AND A REALISATION OF $\pi$
-
- Journal:
- Journal of the London Mathematical Society / Volume 68 / Issue 3 / December 2003
- Published online by Cambridge University Press:
- 17 November 2003, pp. 545-562
- Print publication:
- December 2003
-
- Article
- Export citation
CHARACTERIZING AUTOMORPHISM GROUPS OF ORDERED ABELIAN GROUPS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 35 / Issue 3 / May 2003
- Published online by Cambridge University Press:
- 12 May 2003, pp. 289-292
- Print publication:
- May 2003
-
- Article
- Export citation
Prime Segments of Skew Fields
-
- Journal:
- Canadian Journal of Mathematics / Volume 47 / Issue 6 / 01 December 1995
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1148-1176
- Print publication:
- 01 December 1995
-
- Article
-
- You have access
- Export citation
Soluble Right Orderable Groups are Locally Indicable
-
- Journal:
- Canadian Mathematical Bulletin / Volume 36 / Issue 1 / 01 March 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 22-29
- Print publication:
- 01 March 1993
-
- Article
-
- You have access
- Export citation
Hankel Matrices Over Right Ordered Amenable Groups
-
- Journal:
- Canadian Mathematical Bulletin / Volume 33 / Issue 4 / 01 December 1990
- Published online by Cambridge University Press:
- 20 November 2018, pp. 404-415
- Print publication:
- 01 December 1990
-
- Article
-
- You have access
- Export citation