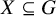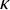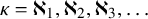Refine search
Actions for selected content:
22 results
A Shelah group in ZFC
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 March 2025, e13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Levy and Thurston obstructions of finite subdivision rules
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 15 December 2023, pp. 2649-2699
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Continuously many quasi-isometry classes of residually finite groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 3 / September 2023
- Published online by Cambridge University Press:
- 19 June 2023, pp. 569-572
- Print publication:
- September 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Commutator length of powers in free products of groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 27 December 2021, pp. 102-119
-
- Article
- Export citation
Generalized small cancellation conditions, non-positive curvature and diagrammatic reducibility
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 152 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 02 March 2021, pp. 545-566
- Print publication:
- June 2022
-
- Article
- Export citation
Relative vertex asphericity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 2 / June 2021
- Published online by Cambridge University Press:
- 16 June 2020, pp. 292-305
- Print publication:
- June 2021
-
- Article
- Export citation
A new test for asphericity and diagrammatic reducibility of group presentations
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 871-895
- Print publication:
- April 2020
-
- Article
- Export citation
Geometry of Infinitely Presented Small Cancellation Groups and Quasi-homomorphisms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 71 / Issue 5 / October 2019
- Published online by Cambridge University Press:
- 09 January 2019, pp. 997-1018
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
Triangles of Baumslag–Solitar Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 64 / Issue 2 / 16 April 2012
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-253
- Print publication:
- 16 April 2012
-
- Article
-
- You have access
- Export citation
Elements of Algebraic Geometry and the Positive Theory of Partially Commutative Groups
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 3 / 01 June 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 481-519
- Print publication:
- 01 June 2010
-
- Article
-
- You have access
- Export citation
EHRLICH’S THEOREM FOR GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 81 / Issue 2 / April 2010
- Published online by Cambridge University Press:
- 13 January 2010, pp. 304-309
- Print publication:
- April 2010
-
- Article
-
- You have access
- Export citation
THE GALLERY LENGTH FILLING FUNCTION AND A GEOMETRIC INEQUALITY FOR FILLING LENGTH
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 92 / Issue 3 / May 2006
- Published online by Cambridge University Press:
- 18 April 2006, pp. 601-623
- Print publication:
- May 2006
-
- Article
- Export citation
the coherence of one-relator groups with torsion and the hanna neumann conjecture
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 37 / Issue 5 / October 2005
- Published online by Cambridge University Press:
- 23 September 2005, pp. 697-705
- Print publication:
- October 2005
-
- Article
- Export citation
SOME DUALITY CONJECTURES FOR FINITE GRAPHS AND THEIR GROUP THEORETIC CONSEQUENCES
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 48 / Issue 2 / June 2005
- Published online by Cambridge University Press:
- 23 May 2005, pp. 389-421
-
- Article
-
- You have access
- Export citation
Approximating Flats by Periodic Flats in CAT(0) Square Complexes
-
- Journal:
- Canadian Journal of Mathematics / Volume 57 / Issue 2 / 01 April 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 416-448
- Print publication:
- 01 April 2005
-
- Article
-
- You have access
- Export citation
ON QUASIVARIETIES OF GROUPS AND EQUATIONS OVER GROUPS
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 37 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 08 February 2005, pp. 67-74
- Print publication:
- January 2005
-
- Article
- Export citation
Bounded rank subgroups of Coxeter groups, Artin groups and one-relator groups with torsion
-
- Journal:
- Proceedings of the London Mathematical Society / Volume 88 / Issue 1 / January 2004
- Published online by Cambridge University Press:
- 13 January 2004, pp. 89-113
- Print publication:
- January 2004
-
- Article
- Export citation
Diagrammatically reducible complexes and Haken manifolds
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 69 / Issue 1 / August 2000
- Published online by Cambridge University Press:
- 09 April 2009, pp. 116-126
- Print publication:
- August 2000
-
- Article
-
- You have access
- Export citation
Second order Dehn functions and HNN-extensions
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 67 / Issue 2 / October 1999
- Published online by Cambridge University Press:
- 09 April 2009, pp. 272-288
- Print publication:
- October 1999
-
- Article
-
- You have access
- Export citation
The Dehn function and a regular set of normal forms for R. Thompson's group F
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society. Series A. Pure Mathematics and Statistics / Volume 62 / Issue 3 / June 1997
- Published online by Cambridge University Press:
- 09 April 2009, pp. 315-328
- Print publication:
- June 1997
-
- Article
-
- You have access
- Export citation