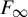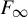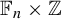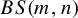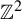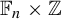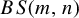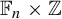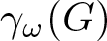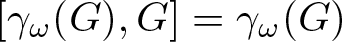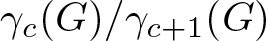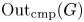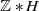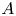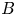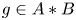Refine search
Actions for selected content:
34 results
A note on the splittings of finitely presented Bestvina–Brady groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 2 / May 2025
- Published online by Cambridge University Press:
- 19 December 2024, pp. 224-227
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cyclic orders and graphs of groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 4 / November 2024
- Published online by Cambridge University Press:
- 21 October 2024, pp. 1125-1136
-
- Article
- Export citation
Centralisers of linear growth automorphisms of free groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 2 / September 2024
- Published online by Cambridge University Press:
- 20 September 2024, pp. 219-240
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hyperbolic one-relator groups
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1-27
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Finitely presented left orderable monsters
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 06 July 2023, pp. 1367-1378
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Strongly aperiodic SFTs on generalized Baumslag–Solitar groups
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 44 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 20 June 2023, pp. 1209-1238
- Print publication:
- May 2024
-
- Article
- Export citation
Baumslag–Solitar groups and residual nilpotence
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 16 June 2023, pp. 532-547
-
- Article
- Export citation
On automorphisms and splittings of special groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 2 / February 2023
- Published online by Cambridge University Press:
- 10 February 2023, pp. 232-305
- Print publication:
- February 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak amenability of free products of hyperbolic and amenable groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 06 January 2022, pp. 698-701
- Print publication:
- September 2022
-
- Article
- Export citation
Commutator length of powers in free products of groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 27 December 2021, pp. 102-119
-
- Article
- Export citation
ON GRAEV’S THEOREM FOR FREE PRODUCTS OF HAUSDORFF TOPOLOGICAL GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 3 / December 2021
- Published online by Cambridge University Press:
- 29 March 2021, pp. 475-483
- Print publication:
- December 2021
-
- Article
- Export citation
ON EXTENSIONS OF PARTIAL ISOMORPHISMS
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 87 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 20 July 2020, pp. 416-435
- Print publication:
- March 2022
-
- Article
- Export citation
Orders on Trees and Free Products of Left-ordered Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 31 March 2020, pp. 335-347
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
On commensurability of right-angled Artin groups II: RAAGs defined by paths
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 170 / Issue 3 / May 2021
- Published online by Cambridge University Press:
- 12 December 2019, pp. 559-608
- Print publication:
- May 2021
-
- Article
- Export citation
INTERSECTIONS OF SUBGROUPS IN VIRTUALLY FREE GROUPS AND VIRTUALLY FREE PRODUCTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 18 July 2019, pp. 266-271
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
ON REGULAR GROUPS AND FIELDS
-
- Journal:
- The Journal of Symbolic Logic / Volume 79 / Issue 3 / September 2014
- Published online by Cambridge University Press:
- 18 August 2014, pp. 826-844
- Print publication:
- September 2014
-
- Article
- Export citation
On Zero-divisors in Group Rings of Groups with Torsion
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 2 / 14 June 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 326-334
- Print publication:
- 14 June 2014
-
- Article
-
- You have access
- Export citation
Infinite presentability of groups and condensation
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 13 / Issue 4 / October 2014
- Published online by Cambridge University Press:
- 02 January 2014, pp. 811-848
- Print publication:
- October 2014
-
- Article
- Export citation
Surface groups within Baumslag doubles
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 54 / Issue 1 / February 2011
- Published online by Cambridge University Press:
- 19 January 2011, pp. 91-97
-
- Article
-
- You have access
- Export citation
RIGIDITY OF GRAPH PRODUCTS OF ABELIAN GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 77 / Issue 2 / April 2008
- Published online by Cambridge University Press:
- 01 April 2008, pp. 187-196
- Print publication:
- April 2008
-
- Article
-
- You have access
- Export citation