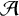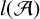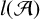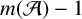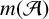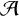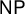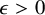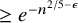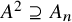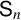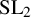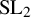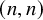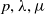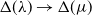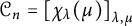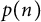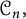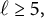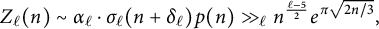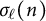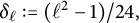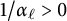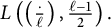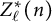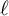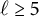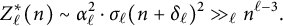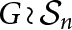Refine search
Actions for selected content:
43 results
The Procesi bundle over the Γ-fixed points of the Hilbert scheme of points in
 $\mathbb{C}^2$
$\mathbb{C}^2$
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 October 2025, pp. 1-33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the central exponent of superalgebras with superinvolution
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 22 September 2025, pp. 1-18
-
- Article
- Export citation
On the structures of the Johnson cokernels of the basis-conjugating automorphism groups of free groups
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 21 July 2025, pp. 1-29
-
- Article
- Export citation
Splines on Cayley graphs of the symmetric group
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 June 2025, e96
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Character and class parameters from entries of character tables of symmetric groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 05 June 2025, pp. 439-447
- Print publication:
- September 2025
-
- Article
- Export citation
On the Aldous-Caputo Spectral Gap Conjecture for Hypergraphs
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 21 May 2025, pp. 259-298
- Print publication:
- September 2025
-
- Article
- Export citation
A combinatorial formula for the nabla operator
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 4 / April 2025
- Published online by Cambridge University Press:
- 17 September 2025, pp. 800-830
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN UPPER BOUND ON THE LENGTH OF AN ALGEBRA AND ITS APPLICATION TO THE GROUP ALGEBRA OF THE DIHEDRAL GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 139-148
- Print publication:
- August 2025
-
- Article
- Export citation
All Kronecker coefficients are reduced Kronecker coefficients
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 November 2024, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
An update on Haiman’s conjectures
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 28 October 2024, e86
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Improved covering results for conjugacy classes of symmetric groups via hypercontractivity
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 21 October 2024, e85
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON MINIMAL DEGREES OF QUOTIENT GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 14 October 2024, pp. 177-179
- Print publication:
- February 2025
-
- Article
-
- You have access
- HTML
- Export citation
COMMON ZEROS OF IRREDUCIBLE CHARACTERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 117 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 11 December 2023, pp. 105-129
- Print publication:
- October 2024
-
- Article
- Export citation
A combinatorial model for the transition matrix between the Specht and
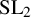 $\operatorname {SL}_2$-web bases
$\operatorname {SL}_2$-web bases
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 20 September 2023, e82
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On homomorphisms into Weyl modules corresponding to partitions with two parts
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 65 / Issue 2 / May 2023
- Published online by Cambridge University Press:
- 11 July 2022, pp. 272-283
- Print publication:
- May 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Zeros in the character tables of symmetric groups with an
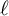 $\ell $-core index
$\ell $-core index
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 27 June 2022, pp. 467-476
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
PRINCIPAL RADICAL SYSTEMS, LEFSCHETZ PROPERTIES, AND PERFECTION OF SPECHT IDEALS OF TWO-ROWED PARTITIONS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 247 / September 2022
- Published online by Cambridge University Press:
- 09 December 2021, pp. 690-730
- Print publication:
- September 2022
-
- Article
- Export citation
1324- and 2143-avoiding Kazhdan–Lusztig immanants and k-positivity
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 14 May 2021, pp. 52-82
- Print publication:
- February 2023
-
- Article
- Export citation
Gelfand Pairs Involving the Wreath Product of Finite Abelian Groups with Symmetric Groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 13 April 2020, pp. 91-97
- Print publication:
- March 2021
-
- Article
- Export citation
The multistep homology of the simplex and representations of symmetric groups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 169 / Issue 2 / September 2020
- Published online by Cambridge University Press:
- 20 June 2019, pp. 231-253
- Print publication:
- September 2020
-
- Article
- Export citation