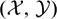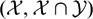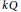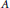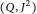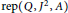Refine search
Actions for selected content:
25 results
Stratifying systems and Jordan-Hölder extriangulated categories
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1-27
-
- Article
- Export citation
A characterisation of higher torsion classes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 07 February 2025, e33
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Resolving dualities and applications to homological invariants
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 22 October 2024, pp. 1-29
-
- Article
- Export citation
Flat model structures and Gorenstein objects in functor categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 14 May 2024, pp. 1-21
-
- Article
- Export citation
Triangular matrix categories over quasi-hereditary categories
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 66 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 21 March 2024, pp. 449-470
- Print publication:
- September 2024
-
- Article
- Export citation
MODEL CATEGORIES AND PRO-p IWAHORI–HECKE MODULES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 04 April 2023, pp. 1029-1076
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
FP-injective dimensions and Gorenstein homology
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 21 December 2022, pp. 1183-1199
-
- Article
- Export citation
ON HIGHER TORSION CLASSES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 10 May 2022, pp. 823-848
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cut cotorsion pairs
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 3 / September 2022
- Published online by Cambridge University Press:
- 10 December 2021, pp. 548-585
- Print publication:
- September 2022
-
- Article
- Export citation
Tilting pairs in extriangulated categories
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 64 / Issue 4 / November 2021
- Published online by Cambridge University Press:
- 26 October 2021, pp. 947-981
-
- Article
- Export citation
HOMOLOGY THEORIES FOR COMPLEXES BASED ON FLATS
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 02 December 2019, pp. 27-44
- Print publication:
- January 2021
-
- Article
- Export citation
Balanced pairs, cotorsion triplets and quiver representations
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 1 / February 2020
- Published online by Cambridge University Press:
- 13 August 2019, pp. 67-90
-
- Article
- Export citation
On triangle equivalences of stable categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 150 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 26 January 2019, pp. 955-974
- Print publication:
- April 2020
-
- Article
- Export citation
GORENSTEIN PROJECTIVE OBJECTS IN FUNCTOR CATEGORIES
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 240 / December 2020
- Published online by Cambridge University Press:
- 26 December 2018, pp. 1-41
- Print publication:
- December 2020
-
- Article
- Export citation
The Gorenstein-projective modules over a monomial algebra
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 02 October 2018, pp. 1115-1134
- Print publication:
- December 2018
-
- Article
- Export citation
GORENSTEIN HOMOLOGICAL PROPERTIES OF TENSOR RINGS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 237 / March 2020
- Published online by Cambridge University Press:
- 07 June 2018, pp. 188-208
- Print publication:
- March 2020
-
- Article
-
- You have access
- HTML
- Export citation
Triangulated Equivalences Involving Gorenstein Projective Modules
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 4 / 01 December 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 879-890
- Print publication:
- 01 December 2017
-
- Article
-
- You have access
- Export citation
Tilting subcategories with respect to cotorsion triples in abelian categories
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 147 / Issue 4 / August 2017
- Published online by Cambridge University Press:
- 28 June 2017, pp. 703-726
- Print publication:
- August 2017
-
- Article
- Export citation
GORENSTEIN MODULES AND GORENSTEIN MODEL STRUCTURES
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 59 / Issue 3 / September 2017
- Published online by Cambridge University Press:
- 27 February 2017, pp. 685-703
- Print publication:
- September 2017
-
- Article
-
- You have access
- Export citation
Exact Morphism Category and Gorenstein-projective Representations
-
- Journal:
- Canadian Mathematical Bulletin / Volume 58 / Issue 4 / 01 December 2015
- Published online by Cambridge University Press:
- 20 November 2018, pp. 824-834
- Print publication:
- 01 December 2015
-
- Article
-
- You have access
- Export citation













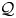






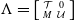
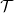
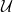
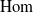
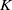
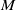
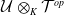
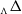
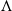

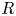
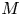
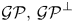
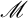
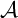
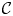
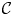
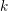
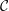
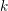
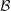
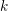
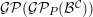
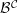
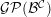
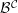
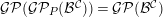
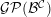
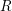
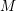

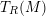
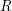
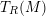
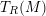
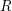

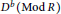
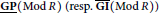
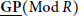
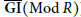
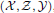 , the notion of
, the notion of 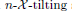 subcategories in an abelian category
subcategories in an abelian category 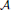 is introduced. It is proved that a virtually Gorenstein ring
is introduced. It is proved that a virtually Gorenstein ring  of Gorenstein injective
of Gorenstein injective 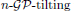 with respect to the cotorsion triple
with respect to the cotorsion triple 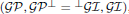 , where
, where 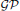 stands for the subcategory of Gorenstein projectives. In the case when a subcategory
stands for the subcategory of Gorenstein projectives. In the case when a subcategory 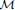 of
of 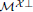 admits a right
admits a right 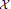 -coresolving covariantly finite and closed under direct summands.
-coresolving covariantly finite and closed under direct summands.