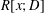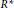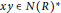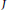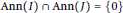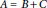Refine search
Actions for selected content:
13 results
On rings which are sums of subrings
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 21 February 2025, pp. 874-882
- Print publication:
- September 2025
-
- Article
- Export citation
The Quantitative Kurosh Problem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 13 February 2025, e42
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
From actions of an abelian group on itself to left braces
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 178 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 09 January 2025, pp. 65-79
- Print publication:
- January 2025
-
- Article
- Export citation
THE PROBABILITY OF ZERO MULTIPLICATION IN FINITE RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 83-88
- Print publication:
- August 2022
-
- Article
- Export citation
ON THE CONNECTION BETWEEN DIFFERENTIAL POLYNOMIAL RINGS AND POLYNOMIAL RINGS OVER NIL RINGS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 3 / June 2020
- Published online by Cambridge University Press:
- 16 September 2019, pp. 438-441
- Print publication:
- June 2020
-
- Article
-
- You have access
- Export citation
Generating Adjoint Groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 62 / Issue 3 / August 2019
- Published online by Cambridge University Press:
- 30 January 2019, pp. 733-738
-
- Article
- Export citation
The Weakly Nilpotent Graph of a Commutative Ring
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 2 / 01 June 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 319-328
- Print publication:
- 01 June 2017
-
- Article
-
- You have access
- Export citation
The Co-annihilating-ideal Graphs of Commutative Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-11
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
A Note on Algebras that are Sums of Two Subalgebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 59 / Issue 2 / 01 June 2016
- Published online by Cambridge University Press:
- 20 November 2018, pp. 340-345
- Print publication:
- 01 June 2016
-
- Article
-
- You have access
- Export citation
JACOBSON RADICAL ALGEBRAS WITH QUADRATIC GROWTH
-
- Journal:
- Glasgow Mathematical Journal / Volume 55 / Issue A / October 2013
- Published online by Cambridge University Press:
- 01 October 2013, pp. 135-147
- Print publication:
- October 2013
-
- Article
-
- You have access
- Export citation
Combinatorics of Words and Semigroup Algebras Which Are Sums of Locally Nilpotent Subalgebras
-
- Journal:
- Canadian Mathematical Bulletin / Volume 47 / Issue 3 / 01 September 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 343-353
- Print publication:
- 01 September 2004
-
- Article
-
- You have access
- Export citation
Radicals and polynomial rings
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 72 / Issue 1 / February 2002
- Published online by Cambridge University Press:
- 09 April 2009, pp. 23-32
- Print publication:
- February 2002
-
- Article
-
- You have access
- Export citation
An Answer to a Question of Kegel on Sums of Rings
-
- Journal:
- Canadian Mathematical Bulletin / Volume 41 / Issue 1 / 01 March 1998
- Published online by Cambridge University Press:
- 20 November 2018, pp. 79-80
- Print publication:
- 01 March 1998
-
- Article
-
- You have access
- Export citation