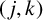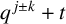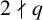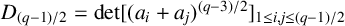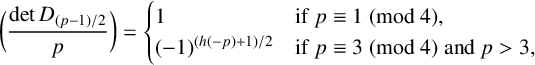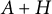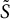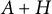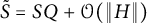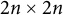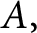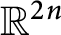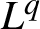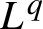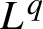Refine search
Actions for selected content:
39 results
Linear damping estimates for periodic roll wave solutions of the inviscid Saint-Venant equations and related systems of hyperbolic balance laws
- Part of
-
- Journal:
- Journal of Nonlinear Waves / Volume 1 / 2025
- Published online by Cambridge University Press:
- 05 December 2025, e21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tunable localisation in parity-time-symmetric resonator arrays with imaginary gauge potentials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 26 September 2025, e157
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Groups of matrices with approximately submultiplicative spectra
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 16 September 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the edge eigenvalues of the precision matrices of nonstationary autoregressive processes
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 57 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 27 May 2025, pp. 907-939
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CHARACTERISTIC POLYNOMIALS OF THE MATRICES WITH
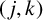 $(\,j,k)$-ENTRY
$(\,j,k)$-ENTRY 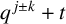 $q^{\,j\pm k}+t$
$q^{\,j\pm k}+t$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 03 June 2024, pp. 228-237
- Print publication:
- April 2025
-
- Article
- Export citation
ON GENERALISED LEGENDRE MATRICES INVOLVING ROOTS OF UNITY OVER FINITE FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 22 April 2024, pp. 199-210
- Print publication:
- October 2024
-
- Article
- Export citation
Block perturbation of symplectic matrices in Williamson’s theorem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 1 / March 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 201-214
- Print publication:
- March 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LEFT AND RIGHT EIGENVECTORS OF A VARIANT OF THE SYLVESTER–KAC MATRIX
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 19 June 2023, pp. 316-326
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE SIZE, SPECTRAL RADIUS, DISTANCE SPECTRAL RADIUS AND FRACTIONAL MATCHINGS IN GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 13 January 2023, pp. 187-199
- Print publication:
- October 2023
-
- Article
- Export citation
Flip signatures
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 43 / Issue 10 / October 2023
- Published online by Cambridge University Press:
- 26 September 2022, pp. 3413-3447
- Print publication:
- October 2023
-
- Article
- Export citation
ON THE NONNEGATIVITY OF THE DIRICHLET ENERGY OF A WEIGHTED GRAPH
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 17 December 2021, pp. 301-305
- Print publication:
- October 2022
-
- Article
- Export citation
AN EIGENVALUE CHARACTERISATION OF THE DUAL EDM CONE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 18 November 2021, pp. 67-69
- Print publication:
- August 2022
-
- Article
- Export citation
Non-negative integral matrices with given spectral radius and controlled dimension
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 42 / Issue 10 / October 2022
- Published online by Cambridge University Press:
- 21 September 2021, pp. 3246-3269
- Print publication:
- October 2022
-
- Article
- Export citation
Spectral gap in random bipartite biregular graphs and applications
- Part of
-
- Journal:
- Combinatorics, Probability and Computing / Volume 31 / Issue 2 / March 2022
- Published online by Cambridge University Press:
- 23 July 2021, pp. 229-267
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
STRUCTURED SINGULAR VALUES OF SOME GENERALISED STOCHASTIC MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 09 July 2021, pp. 58-67
- Print publication:
- February 2022
-
- Article
- Export citation
Spectral distribution of symmetrized circulant matrices
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 03 June 2021, pp. 431-446
- Print publication:
- June 2022
-
- Article
- Export citation
Derivatives of symplectic eigenvalues and a Lidskii type theorem
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 02 December 2020, pp. 457-485
- Print publication:
- April 2022
-
- Article
-
- You have access
- Export citation
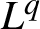 $L^{q}$-spectra of measures on planar non-conformal attractors
$L^{q}$-spectra of measures on planar non-conformal attractors
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 41 / Issue 11 / November 2021
- Published online by Cambridge University Press:
- 26 October 2020, pp. 3288-3306
- Print publication:
- November 2021
-
- Article
- Export citation
Solution of a Nonlinear Eigenvalue Problem Using Signed Singular Values
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2018, pp. 799-809
- Print publication:
- November 2017
-
- Article
- Export citation
Integrable Properties of a Variant of the Discrete Hungry Toda Equations and Their Relationship to Eigenpairs of Band Matrices
- Part of
-
- Journal:
- East Asian Journal on Applied Mathematics / Volume 7 / Issue 4 / November 2017
- Published online by Cambridge University Press:
- 31 January 2018, pp. 785-798
- Print publication:
- November 2017
-
- Article
- Export citation