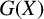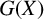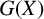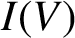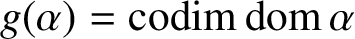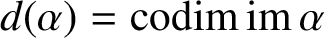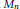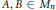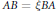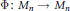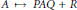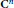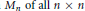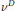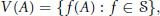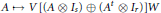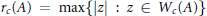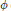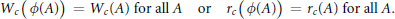Refine search
Actions for selected content:
13 results
MAXIMAL SUBSEMIGROUPS OF INFINITE SYMMETRIC GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 29 January 2024, pp. 324-337
- Print publication:
- October 2024
-
- Article
- Export citation
INJECTIVE LINEAR TRANSFORMATIONS WITH EQUAL GAP AND DEFECT
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 18 May 2021, pp. 106-116
- Print publication:
- February 2022
-
- Article
- Export citation
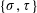 $\{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\}$-Rota–Baxter Operators, Infinitesimal Hom-bialgebras and the Associative (Bi)Hom-Yang–Baxter Equation
$\{\unicode[STIX]{x1D70E},\unicode[STIX]{x1D70F}\}$-Rota–Baxter Operators, Infinitesimal Hom-bialgebras and the Associative (Bi)Hom-Yang–Baxter Equation
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 62 / Issue 2 / June 2019
- Published online by Cambridge University Press:
- 07 January 2019, pp. 355-372
- Print publication:
- June 2019
-
- Article
-
- You have access
- Export citation
Cross-Commodity Spot Price Modeling with Stochastic Volatility and Leverage For Energy Markets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 22 February 2016, pp. 545-571
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
Pricing of Forwards and Options in a Multivariate Non-Gaussian Stochastic Volatility Model for Energy Markets
- Part of
-
- Journal:
- Advances in Applied Probability / Volume 45 / Issue 2 / June 2013
- Published online by Cambridge University Press:
- 22 February 2016, pp. 572-594
- Print publication:
- June 2013
-
- Article
-
- You have access
- Export citation
General Preservers of Quasi-Commutativity
-
- Journal:
- Canadian Journal of Mathematics / Volume 62 / Issue 4 / 01 August 2010
- Published online by Cambridge University Press:
- 20 November 2018, pp. 758-786
- Print publication:
- 01 August 2010
-
- Article
-
- You have access
- Export citation
Adjacency Preserving Maps on Hermitian Matrices
-
- Journal:
- Canadian Journal of Mathematics / Volume 60 / Issue 5 / October 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1050-1066
- Print publication:
- October 2008
-
- Article
-
- You have access
- Export citation
Continuous Adjacency Preserving Maps on Real Matrices
-
- Journal:
- Canadian Mathematical Bulletin / Volume 48 / Issue 2 / 01 June 2005
- Published online by Cambridge University Press:
- 20 November 2018, pp. 267-274
- Print publication:
- 01 June 2005
-
- Article
-
- You have access
- Export citation
LINEAR AUTOMORPHISMS THAT ARE SYMPLECTOMORPHISMS
-
- Journal:
- Journal of the London Mathematical Society / Volume 69 / Issue 2 / April 2004
- Published online by Cambridge University Press:
- 29 March 2004, pp. 503-517
- Print publication:
- April 2004
-
- Article
- Export citation
Linear Operators on Matrix Algebras that Preserve the Numerical Range, Numerical Radius or the States
-
- Journal:
- Canadian Journal of Mathematics / Volume 56 / Issue 1 / 01 February 2004
- Published online by Cambridge University Press:
- 20 November 2018, pp. 134-167
- Print publication:
- 01 February 2004
-
- Article
-
- You have access
- Export citation
Linear Maps Transforming the Unitary Group
-
- Journal:
- Canadian Mathematical Bulletin / Volume 46 / Issue 1 / 01 March 2003
- Published online by Cambridge University Press:
- 20 November 2018, pp. 54-58
- Print publication:
- 01 March 2003
-
- Article
-
- You have access
- Export citation
Linear Operators Preserving Generalized Numerical Ranges and Radii on Certain Triangular Algebras of Matrices
-
- Journal:
- Canadian Mathematical Bulletin / Volume 44 / Issue 3 / 01 September 2001
- Published online by Cambridge University Press:
- 20 November 2018, pp. 270-281
- Print publication:
- 01 September 2001
-
- Article
-
- You have access
- Export citation
Mappings which Preserve Idempotents, Local Automorphisms, and Local Derivations
-
- Journal:
- Canadian Journal of Mathematics / Volume 45 / Issue 3 / 01 June 1993
- Published online by Cambridge University Press:
- 20 November 2018, pp. 483-496
- Print publication:
- 01 June 1993
-
- Article
-
- You have access
- Export citation