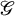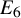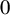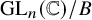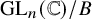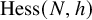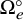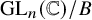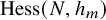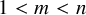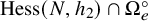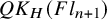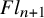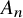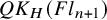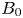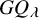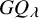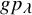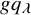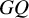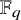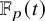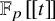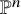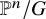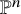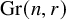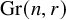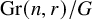Refine search
Actions for selected content:
78 results
Quantum K theory of Grassmannians, Wilson line operators and Schur bundles
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 04 September 2025, e140
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the formal Peterson subalgebra and its dual
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-21
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Smooth locus of twisted affine Schubert varieties and twisted affine Demazure modules
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 July 2025, e121
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Tilting sheaves for real groups and Koszul duality
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 7 / July 2025
- Published online by Cambridge University Press:
- 11 September 2025, pp. 1698-1777
- Print publication:
- July 2025
-
- Article
- Export citation
K-Orbit closures and Hessenberg varieties
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 June 2025, e103
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Newell–Littlewood numbers III: Eigencones and GIT-semigroups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 5 / May 2025
- Published online by Cambridge University Press:
- 27 August 2025, pp. 1054-1074
- Print publication:
- May 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A categorical action of the shifted
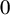 $0$-affine algebra
$0$-affine algebra
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 15 April 2025, e74
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Coordinate rings of regular nilpotent Hessenberg varieties in the open opposite schubert cell
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 17 February 2025, e44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Geometrization of the Satake transform for mod p Hecke algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 05 February 2025, e26
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A presentation of the torus-equivariant quantum K-theory ring of flag manifolds of type A, Part II: quantum double Grothendieck polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 January 2025, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Generic stabilizers for simple algebraic groups acting on orthogonal and symplectic Grassmannians
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 24 January 2025, e8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
4-Torsion classes in the integral cohomology of oriented Grassmannians
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 15 January 2025, pp. 1-43
-
- Article
- Export citation
A new generic vanishing theorem on homogeneous varieties and the positivity conjecture for triple intersections of Schubert cells
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 10 March 2025, pp. 1-12
- Print publication:
- January 2025
-
- Article
- Export citation
An inverse Grassmannian Littlewood–Richardson rule and extensions
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 03 December 2024, e114
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Combinatorial formulas for shifted dual stable Grothendieck polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 13 February 2024, e22
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Δ–Springer varieties and Hall–Littlewood polynomials
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 31 January 2024, e19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Double Schubert polynomials do have saturated Newton polytopes
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 November 2023, e100
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Grassmanniennes affines tordues sur les entiers
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 23 February 2023, e12
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Relative Richardson varieties
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 1 / July 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. 161-186
- Print publication:
- July 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Unwinding Toric Degenerations and Mirror Symmetry for Grassmannians
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 14 December 2022, e111
-
- Article
-
- You have access
- Open access
- HTML
- Export citation