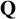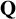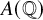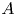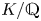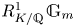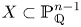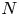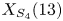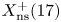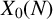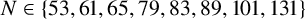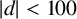Refine search
Actions for selected content:
72 results
ON THE DESCENT CONJECTURE FOR RATIONAL POINTS AND ZERO-CYCLES
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu , First View
- Published online by Cambridge University Press:
- 19 November 2025, pp. 1-49
-
- Article
- Export citation
Improvements on dimension growth results and effective Hilbert’s irreducibility theorem
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 19 September 2025, e153
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
POLYNOMIALS REPRESENTED BY NORM FORMS VIA THE BETA SIEVE
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 4 / July 2025
- Published online by Cambridge University Press:
- 25 February 2025, pp. 1463-1519
- Print publication:
- July 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Average Analytic Ranks of Elliptic Curves over Number Fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 11 February 2025, e40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Complete verification of strong BSD for many modular abelian surfaces over
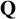 ${\mathbf {Q}}$
${\mathbf {Q}}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 30 January 2025, e20
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
AN UPPER BOUND FOR THE GENERALISED GREATEST COMMON DIVISOR OF RATIONAL POINTS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 248-253
- Print publication:
- October 2025
-
- Article
- Export citation
Torsion points and concurrent exceptional curves on del Pezzo surfaces of degree one
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 2 / June 2025
- Published online by Cambridge University Press:
- 12 December 2024, pp. 634-652
- Print publication:
- June 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Rational torsion points on abelian surfaces with quaternionic multiplication
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 08 November 2024, e92
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weak approximation on the norm one torus
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 6 / June 2024
- Published online by Cambridge University Press:
- 06 May 2024, pp. 1304-1348
- Print publication:
- June 2024
-
- Article
- Export citation
GENERALISED QUADRATIC FORMS OVER TOTALLY REAL NUMBER FIELDS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 6 / November 2024
- Published online by Cambridge University Press:
- 11 April 2024, pp. 2859-2912
- Print publication:
- November 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Hasse principle for complete intersections
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 05 March 2024, pp. 771-835
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Most odd-degree binary forms fail to primitively represent a square
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 3 / March 2024
- Published online by Cambridge University Press:
- 08 February 2024, pp. 481-517
- Print publication:
- March 2024
-
- Article
- Export citation
Heights and quantitative arithmetic on stacky curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 19 January 2024, pp. 481-534
- Print publication:
- April 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Manin–Peyre conjecture for smooth spherical Fano varieties of semisimple rank one
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 18 January 2024, e11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hensel minimality II: Mixed characteristic and a diophantine application
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 October 2023, e89
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Quartic and Quintic Hypersurfaces with Dense Rational Points
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 27 June 2023, e55
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weight filtrations on Selmer schemes and the effective Chabauty–Kim method
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 7 / July 2023
- Published online by Cambridge University Press:
- 20 June 2023, pp. 1531-1605
- Print publication:
- July 2023
-
- Article
- Export citation
Quadratic Chabauty for modular curves: algorithms and examples
- Part of
-
- Journal:
- Compositio Mathematica / Volume 159 / Issue 6 / June 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 1111-1152
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COMPUTING POINTS ON BIELLIPTIC MODULAR CURVES OVER FIXED QUADRATIC FIELDS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 20 April 2023, pp. 6-13
- Print publication:
- February 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Heights on stacks and a generalized Batyrev–Manin–Malle conjecture
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 03 March 2023, e14
-
- Article
-
- You have access
- Open access
- HTML
- Export citation