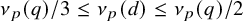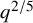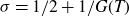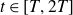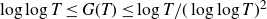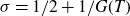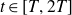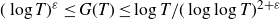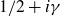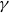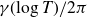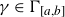Refine search
Actions for selected content:
86 results
A note on twisted moments of Dirichlet
 $\boldsymbol{L}$-functions
$\boldsymbol{L}$-functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal , First View
- Published online by Cambridge University Press:
- 24 September 2025, pp. 1-8
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On moments of L-functions over Dirichlet characters
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 19 September 2025, pp. 1-24
-
- Article
- Export citation
Oscillation results for the summatory functions of fake
 $\mu $’s
$\mu $’s
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 August 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Limit theorems for a class of unbounded observables with an application to ‘Sampling the Lindelöf hypothesis’
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 46 / Issue 1 / January 2026
- Published online by Cambridge University Press:
- 12 August 2025, pp. 34-92
- Print publication:
- January 2026
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Counting cyclic extensions with local conditions and applications to L-values in the critical strip
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 08 August 2025, pp. 1-39
-
- Article
- Export citation
AN ASYMPTOTIC ESTIMATE FOR THE CHARACTERISTIC AND NUMBER OF FIXED POINTS OF THE RIEMANN ZETA FUNCTION
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 260 / December 2025
- Published online by Cambridge University Press:
- 01 August 2025, pp. 648-665
- Print publication:
- December 2025
-
- Article
- Export citation
A criterion for the simple normality of fractional powers of two via the Riemann zeta function
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 29 May 2025, pp. 1-24
-
- Article
- Export citation
Euler Products at the Centre and Applications to Chebyshev’s Bias
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 27 May 2025, pp. 331-349
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotic second moment of Dirichlet L-functions along a thin coset
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 02 May 2025, e83
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Shifted moments of quadratic Dirichlet L-functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 4 / December 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 1116-1143
- Print publication:
- December 2025
-
- Article
- Export citation
ON SOME EFFECTIVE RESULTS INVOLVING ZEROS OF THE RIEMANN ZETA FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 21 March 2025, pp. 563-565
- Print publication:
- June 2025
-
- Article
-
- You have access
- HTML
- Export citation
Equivalence between the functional equation and Voronoï-type summation identities for a class of L-functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics , First View
- Published online by Cambridge University Press:
- 25 November 2024, pp. 1-41
-
- Article
- Export citation
Discrepancy bounds for the distribution of L-functions near the critical line
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 2 / September 2024
- Published online by Cambridge University Press:
- 21 October 2024, pp. 313-332
- Print publication:
- September 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal subfields of elliptic curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 22 May 2024, pp. 1029-1045
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BOUNDS FOR MOMENTS OF QUADRATIC DIRICHLET CHARACTER SUMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 06 May 2024, pp. 43-47
- Print publication:
- February 2025
-
- Article
- Export citation
Omega results for the error term in the square-free divisor problem for square-full integers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 20 March 2024, pp. 1011-1028
- Print publication:
- December 2024
-
- Article
- Export citation
The uniform distribution modulo one of certain subsequences of ordinates of zeros of the zeta function
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 01 March 2024, pp. 593-608
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Remarks on a formula of Ramanujan
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 4 / August 2025
- Published online by Cambridge University Press:
- 06 February 2024, pp. 1543-1554
- Print publication:
- August 2025
-
- Article
- Export citation
BOUNDING ZETA ON THE 1-LINE UNDER THE PARTIAL RIEMANN HYPOTHESIS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 10 January 2024, pp. 244-251
- Print publication:
- October 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
NEW EFFECTIVE RESULTS IN THE THEORY OF THE RIEMANN ZETA-FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 12 December 2023, pp. 403-406
- Print publication:
- April 2024
-
- Article
-
- You have access
- HTML
- Export citation