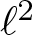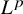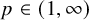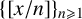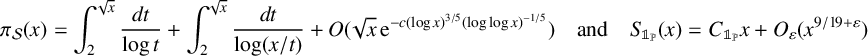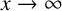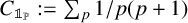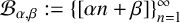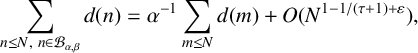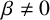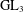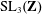Refine search
Actions for selected content:
62 results
SUMS OF KLOOSTERMAN SUMS OVER SQUARE-FREE AND SMOOTH INTEGERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 20 November 2025, pp. 1-13
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cancellation in sums over special sequences on
 $\mathrm {GL}_m$ and their applications
$\mathrm {GL}_m$ and their applications
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 August 2025, pp. 1-30
-
- Article
- Export citation
On a theorem of Mattila in the finite p-adic setting
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 14 July 2025, pp. 1-15
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
BINARY AND TERNARY CONGRUENCES INVOLVING INTERVALS AND SETS MODULO A PRIME
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 18 March 2025, pp. 237-247
- Print publication:
- October 2025
-
- Article
- Export citation
Semisimple random walks on the torus
- Part of
-
- Journal:
- Ergodic Theory and Dynamical Systems / Volume 45 / Issue 10 / October 2025
- Published online by Cambridge University Press:
- 03 March 2025, pp. 3090-3147
- Print publication:
- October 2025
-
- Article
- Export citation
EXISTENCE OF K-MULTIMAGIC SQUARES AND MAGIC SQUARES OF kth POWERS WITH DISTINCT ENTRIES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 3 / December 2025
- Published online by Cambridge University Press:
- 11 February 2025, pp. 441-448
- Print publication:
- December 2025
-
- Article
- Export citation
Exponential sums over Möbius convolutions with applications to partitions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-36
-
- Article
- Export citation
Full Poissonian local statistics of slowly growing sequences
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 24 March 2025, pp. 148-180
- Print publication:
- January 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
L2 to Lp bounds for spectral projectors on the Euclidean two-dimensional torus
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 67 / Issue 2 / May 2024
- Published online by Cambridge University Press:
- 15 March 2024, pp. 431-459
-
- Article
- Export citation
ENERGY BOUNDS FOR MODULAR ROOTS AND THEIR APPLICATIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 04 March 2024, pp. 1765-1806
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On a multi-parameter variant of the Bellow–Furstenberg problem
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 September 2023, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrete restriction estimates for forms in many variables
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 18 September 2023, pp. 923-939
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Weil Sums over Small Subgroups
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 15 August 2023, pp. 39-53
- Print publication:
- January 2024
-
- Article
- Export citation
ON THE PRIMES IN FLOOR FUNCTION SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 2 / October 2023
- Published online by Cambridge University Press:
- 23 November 2022, pp. 236-243
- Print publication:
- October 2023
-
- Article
- Export citation
Bounds for spectral projectors on tori
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 12 May 2022, e24
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON THE DIVISOR FUNCTION OVER NONHOMOGENEOUS BEATTY SEQUENCES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 04 March 2022, pp. 280-287
- Print publication:
- October 2022
-
- Article
- Export citation
EXPONENTIAL SUMS AND ADDITIVE COMBINATORICS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 103 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 09 November 2020, pp. 506-508
- Print publication:
- June 2021
-
- Article
-
- You have access
- Export citation
Möbius Randomness Law for Frobenius Traces of Ordinary Curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 64 / Issue 1 / March 2021
- Published online by Cambridge University Press:
- 15 May 2020, pp. 192-203
- Print publication:
- March 2021
-
- Article
- Export citation
PERIODIC TWISTS OF
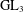 $\operatorname{GL}_{3}$-AUTOMORPHIC FORMS
$\operatorname{GL}_{3}$-AUTOMORPHIC FORMS
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 8 / 2020
- Published online by Cambridge University Press:
- 12 March 2020, e15
-
- Article
-
- You have access
- Open access
- Export citation
IGUSA’S CONJECTURE FOR EXPONENTIAL SUMS: OPTIMAL ESTIMATES FOR NONRATIONAL SINGULARITIES
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 7 / 2019
- Published online by Cambridge University Press:
- 31 July 2019, e3
-
- Article
-
- You have access
- Open access
- Export citation