Refine search
Actions for selected content:
18 results
ON SOME EFFECTIVE RESULTS INVOLVING ZEROS OF THE RIEMANN ZETA FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 21 March 2025, pp. 563-565
- Print publication:
- June 2025
-
- Article
-
- You have access
- HTML
- Export citation
Exponential sums over Möbius convolutions with applications to partitions
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 09 January 2025, pp. 1-36
-
- Article
- Export citation
On a multi-parameter variant of the Bellow–Furstenberg problem
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 19 September 2023, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON MÖBIUS DISJOINTNESS FOR SKEW PRODUCTS ON A CIRCLE AND A NILMANIFOLD
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 3 / June 2023
- Published online by Cambridge University Press:
- 04 October 2022, pp. 471-482
- Print publication:
- June 2023
-
- Article
- Export citation
On the structure of spectral and tiling subsets of cyclic groups
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 10 May 2022, e23
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
DISTRIBUTION OF ELEMENTS OF A FLOOR FUNCTION SET IN ARITHMETICAL PROGRESSIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 01 March 2022, pp. 419-424
- Print publication:
- December 2022
-
- Article
- Export citation
SUMS OF POLYNOMIAL-TYPE EXCEPTIONAL UNITS MODULO
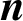 $\boldsymbol {n}$
$\boldsymbol {n}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 21 July 2021, pp. 202-211
- Print publication:
- April 2022
-
- Article
- Export citation
The distribution of the maximum of partial sums of Kloosterman sums and other trace functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 157 / Issue 7 / July 2021
- Published online by Cambridge University Press:
- 28 June 2021, pp. 1610-1651
- Print publication:
- July 2021
-
- Article
- Export citation
Une note sur la densité des zéros des sommes partielles de la fonction zeta de Dedekind sur un corps quadratique
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 2 / June 2022
- Published online by Cambridge University Press:
- 24 May 2021, pp. 409-415
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the size of the maximum of incomplete Kloosterman sums
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 172 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 15 April 2021, pp. 563-590
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
A LOWER BOUND FOR THE LARGE SIEVE WITH SQUARE MODULI
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 27 February 2019, pp. 225-229
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation
The Rudin–Shapiro Sequence and Similar Sequences Are Normal Along Squares
-
- Journal:
- Canadian Journal of Mathematics / Volume 70 / Issue 5 / 01 October 2018
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1096-1129
- Print publication:
- 01 October 2018
-
- Article
-
- You have access
- Export citation
ON THE DISTRIBUTION OF THE MAXIMUM OF CUBIC EXPONENTIAL SUMS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 19 / Issue 4 / July 2020
- Published online by Cambridge University Press:
- 27 September 2018, pp. 1259-1286
- Print publication:
- July 2020
-
- Article
- Export citation
Sub-Weyl subconvexity for Dirichlet
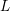 $L$-functions to prime power moduli
$L$-functions to prime power moduli
- Part of
-
- Journal:
- Compositio Mathematica / Volume 152 / Issue 4 / April 2016
- Published online by Cambridge University Press:
- 03 November 2015, pp. 825-875
- Print publication:
- April 2016
-
- Article
- Export citation
Primes with an average sum of digits
- Part of
-
- Journal:
- Compositio Mathematica / Volume 145 / Issue 2 / March 2009
- Published online by Cambridge University Press:
- 01 March 2009, pp. 271-292
- Print publication:
- March 2009
-
- Article
-
- You have access
- Export citation
Purity of exponential sums on $\mathbb{A}^n$
-
- Journal:
- Compositio Mathematica / Volume 142 / Issue 2 / March 2006
- Published online by Cambridge University Press:
- 13 March 2006, pp. 295-306
- Print publication:
- March 2006
-
- Article
-
- You have access
- Export citation
On a question of Igusa, II: Uniform asymptotic bounds for Fourier transforms in several variables
-
- Journal:
- Compositio Mathematica / Volume 141 / Issue 1 / January 2005
- Published online by Cambridge University Press:
- 01 December 2004, pp. 192-226
- Print publication:
- January 2005
-
- Article
-
- You have access
- Export citation
BOUNDS ON EXPONENTIAL SUMS AND THE POLYNOMIAL WARING PROBLEM MOD p
-
- Journal:
- Journal of the London Mathematical Society / Volume 67 / Issue 2 / April 2003
- Published online by Cambridge University Press:
- 25 March 2003, pp. 319-336
- Print publication:
- April 2003
-
- Article
- Export citation
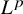
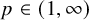
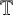
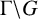
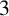
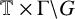
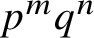
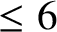
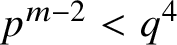
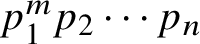
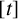
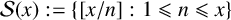
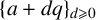
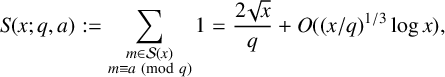
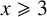
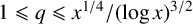
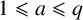
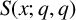
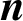
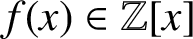
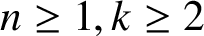
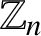
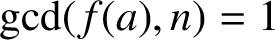
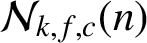

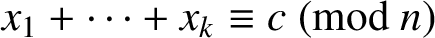
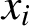
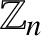
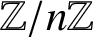
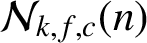
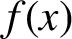
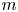
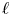
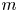
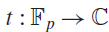
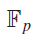
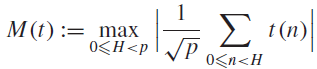
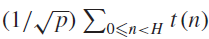
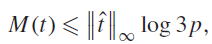
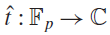
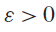
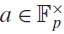
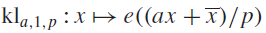
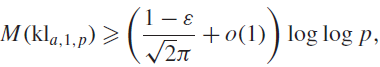

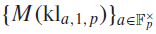
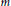

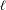
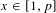
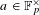
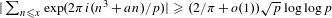
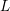
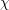
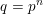
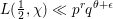

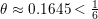
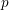
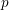
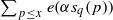 (where the sum is restricted to
(where the sum is restricted to 