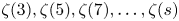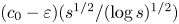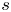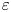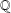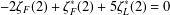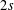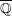Refine search
Actions for selected content:
16 results
IRRATIONALITY OF ZEROS OF POLYGAMMA FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 10 February 2025, pp. 1-11
-
- Article
- Export citation
Semiabelian varieties and transcendence on Weierstrass sigma functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 1 / January 2025
- Published online by Cambridge University Press:
- 25 November 2024, pp. 107-113
- Print publication:
- January 2025
-
- Article
- Export citation
Linear independence of series related to the Thue–Morse sequence along powers
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 3 / September 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 822-832
- Print publication:
- September 2024
-
- Article
- Export citation
LINEAR INDEPENDENCE OF VALUES OF THE q-EXPONENTIAL AND RELATED FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 23 October 2023, pp. 453-463
- Print publication:
- June 2024
-
- Article
- Export citation
Every Salem number is a difference of two Pisot numbers
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 08 August 2023, pp. 862-867
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on spaces of almost periodic functions with values in Banach spaces
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 18 January 2022, pp. 953-962
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A note on the number of irrational odd zeta values
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 8 / August 2020
- Published online by Cambridge University Press:
- 09 October 2020, pp. 1699-1717
- Print publication:
- August 2020
-
- Article
- Export citation
ON LINEAR RELATIONS FOR DIRICHLET SERIES FORMED BY RECURSIVE SEQUENCES OF SECOND ORDER
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 110 / Issue 3 / June 2021
- Published online by Cambridge University Press:
- 16 January 2020, pp. 406-430
- Print publication:
- June 2021
-
- Article
- Export citation
Linear Independence of Logarithms of Cyclotomic Numbers and a Conjecture of Livingston
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 1 / March 2020
- Published online by Cambridge University Press:
- 12 December 2019, pp. 31-45
- Print publication:
- March 2020
-
- Article
-
- You have access
- Export citation
On linear independence measures of the values of Mahler functions
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 148 / Issue 6 / December 2018
- Published online by Cambridge University Press:
- 22 June 2018, pp. 1297-1311
- Print publication:
- December 2018
-
- Article
- Export citation
On a Conjecture of Livingston
-
- Journal:
- Canadian Mathematical Bulletin / Volume 60 / Issue 1 / 01 March 2017
- Published online by Cambridge University Press:
- 20 November 2018, pp. 184-195
- Print publication:
- 01 March 2017
-
- Article
-
- You have access
- Export citation
An explicit Baker-type lower bound of exponential values
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 145 / Issue 6 / December 2015
- Published online by Cambridge University Press:
- 27 October 2015, pp. 1153-1182
- Print publication:
- December 2015
-
- Article
- Export citation
IRRATIONALITY AND NONQUADRATICITY MEASURES FOR LOGARITHMS OF ALGEBRAIC NUMBERS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 92 / Issue 2 / April 2012
- Published online by Cambridge University Press:
- 22 November 2012, pp. 237-267
- Print publication:
- April 2012
-
- Article
-
- You have access
- Export citation
Simultaneous Polynomial Approximations of the Lerch Function
-
- Journal:
- Canadian Journal of Mathematics / Volume 61 / Issue 6 / 01 December 2009
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1341-1356
- Print publication:
- 01 December 2009
-
- Article
-
- You have access
- Export citation
On Linear Independence of a Certain Multivariate Infinite Product
-
- Journal:
- Canadian Mathematical Bulletin / Volume 51 / Issue 1 / 01 March 2008
- Published online by Cambridge University Press:
- 20 November 2018, pp. 32-46
- Print publication:
- 01 March 2008
-
- Article
-
- You have access
- Export citation
ARITHMETICAL RESULTS ON CERTAIN MULTIVARIATE POWER SERIES
-
- Journal:
- Bulletin of the London Mathematical Society / Volume 38 / Issue 2 / April 2006
- Published online by Cambridge University Press:
- 16 March 2006, pp. 192-200
- Print publication:
- April 2006
-
- Article
- Export citation