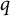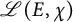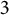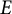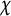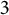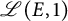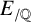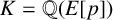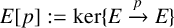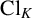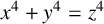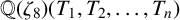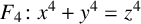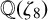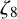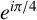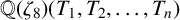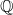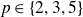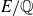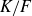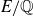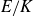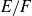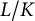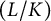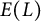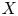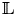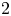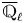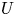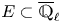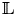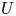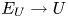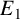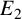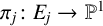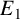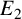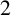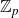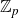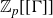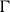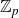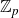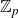Refine search
Actions for selected content:
141 results
Improved bounds for Serre’s open image theorem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 10 September 2025, pp. 1-19
-
- Article
- Export citation
Elliptic curves and spin
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 11 July 2025, pp. 519-539
- Print publication:
- November 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Opposing average congruence class biases in the cyclicity and Koblitz conjectures for elliptic curves
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 June 2025, pp. 1-51
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On L-values of elliptic curves twisted by cubic Dirichlet characters
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 20 June 2025, pp. 1-25
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Class groups and Selmer groups in special families
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 10 June 2025, pp. 1-23
-
- Article
- Export citation
Theory of heat equations for sigma functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 28 February 2025, pp. 365-422
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Hilbert’s 10th problem via Mordell curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 26 February 2025, pp. 939-949
- Print publication:
- September 2025
-
- Article
- Export citation
Average Analytic Ranks of Elliptic Curves over Number Fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 11 February 2025, e40
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON PSEUDO-NULLITY OF THE FINE MORDELL–WEIL GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 03 February 2025, pp. 71-79
- Print publication:
- August 2025
-
- Article
- Export citation
LOW RANK SPECIALISATIONS OF ELLIPTIC SURFACES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 1 / August 2025
- Published online by Cambridge University Press:
- 13 January 2025, pp. 118-127
- Print publication:
- August 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CLASS GROUP STATISTICS FOR TORSION FIELDS GENERATED BY ELLIPTIC CURVES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 118 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 02 December 2024, pp. 245-264
- Print publication:
- April 2025
-
- Article
- Export citation
POINTS ON
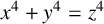 $x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF
$x^4+y^4=z^4$ OVER QUADRATIC EXTENSIONS OF 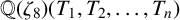 ${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
${\mathbb {Q}}(\zeta _8)(T_1,T_2,\ldots ,T_n)$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 07 November 2024, pp. 19-31
- Print publication:
- February 2025
-
- Article
- Export citation
THEOREM OF WARD ON SYMMETRIES OF ELLIPTIC NETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 93-106
- Print publication:
- February 2025
-
- Article
- Export citation
The Failure of Galois Descent for p-Selmer Groups of Elliptic Curves
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 177 / Issue 1 / July 2024
- Published online by Cambridge University Press:
- 19 September 2024, pp. 185-218
- Print publication:
- July 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Minimal subfields of elliptic curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 22 May 2024, pp. 1029-1045
- Print publication:
- December 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The Heisenberg covering of the Fermat curve
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1637-1663
- Print publication:
- October 2025
-
- Article
- Export citation
Constructing abelian varieties from rank 2 Galois representations
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 4 / April 2024
- Published online by Cambridge University Press:
- 07 March 2024, pp. 709-731
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Common valuations of division polynomials
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 155 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 26 February 2024, pp. 1646-1660
- Print publication:
- October 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
INTERSECTING THE TORSION OF ELLIPTIC CURVES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 1 / August 2024
- Published online by Cambridge University Press:
- 27 December 2023, pp. 56-63
- Print publication:
- August 2024
-
- Article
- Export citation
Structure of fine Selmer groups over
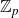 $\mathbb{Z}_{p}$-extensions
$\mathbb{Z}_{p}$-extensions
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 2 / March 2024
- Published online by Cambridge University Press:
- 04 October 2023, pp. 287-308
- Print publication:
- March 2024
-
- Article
- Export citation