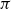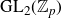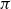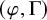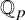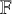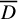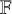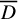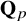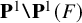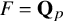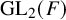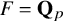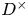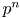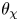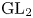Refine search
Actions for selected content:
53 results
Quasi-polynomial representations of double affine Hecke algebras
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 16 April 2025, e73
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
 $ \epsilon $-ISOMORPHISMS FOR RANK ONE
$ \epsilon $-ISOMORPHISMS FOR RANK ONE  $( \varphi , \Gamma )$-MODULES OVER LUBIN-TATE ROBBA RINGS
$( \varphi , \Gamma )$-MODULES OVER LUBIN-TATE ROBBA RINGS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 11 April 2025, pp. 1895-1994
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the
 $\mu$-invariant of two-variable
$\mu$-invariant of two-variable  $2$-adic
$2$-adic  $\boldsymbol{L}$-functions
$\boldsymbol{L}$-functions
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 67 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 24 February 2025, pp. 325-355
- Print publication:
- September 2025
-
- Article
- Export citation
Cuspidal
 ${\ell }$-modular representations of
${\ell }$-modular representations of  $\operatorname {GL}_n({ F})$ distinguished by a Galois involution
$\operatorname {GL}_n({ F})$ distinguished by a Galois involution
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 20 February 2025, e48
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On local Galois deformation rings: generalised tori
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 18 February 2025, e45
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stability in the category of smooth mod-p representations of
 ${\mathrm {SL}}_2(\mathbb {Q}_p)$
${\mathrm {SL}}_2(\mathbb {Q}_p)$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 09 September 2024, e77
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
The sup-norm problem beyond the newform
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 176 / Issue 3 / May 2024
- Published online by Cambridge University Press:
- 12 March 2024, pp. 517-545
- Print publication:
- May 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modularity of trianguline Galois representations
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 05 January 2024, e3
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Slopes in eigenvarieties for definite unitary groups
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 1 / January 2024
- Published online by Cambridge University Press:
- 22 November 2023, pp. 52-89
- Print publication:
- January 2024
-
- Article
- Export citation
Equidimensionality of universal pseudodeformation rings in characteristic p for absolute Galois groups of p-adic fields
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 17 November 2023, e102
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On local Galois deformation rings
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 26 October 2023, e30
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE DIAGONAL CYCLE EULER SYSTEM FOR
 $\mathrm {GL}_2\times \mathrm {GL}_2$
$\mathrm {GL}_2\times \mathrm {GL}_2$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 5 / September 2025
- Published online by Cambridge University Press:
- 13 June 2023, pp. 1591-1653
- Print publication:
- September 2025
-
- Article
- Export citation
Factorisation de la cohomologie étale p-adique de la tour de Drinfeld
- Part of
-
- Journal:
- Forum of Mathematics, Pi / Volume 11 / 2023
- Published online by Cambridge University Press:
- 26 May 2023, e16
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A
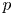 $p$-adic monodromy theorem for de Rham local systems
$p$-adic monodromy theorem for de Rham local systems
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 12 / December 2022
- Published online by Cambridge University Press:
- 15 December 2022, pp. 2157-2205
- Print publication:
- December 2022
-
- Article
- Export citation
REDUCTIONS OF
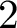 $2$-DIMENSIONAL SEMISTABLE REPRESENTATIONS WITH LARGE
$2$-DIMENSIONAL SEMISTABLE REPRESENTATIONS WITH LARGE  $\mathcal L$-INVARIANT
$\mathcal L$-INVARIANT
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 6 / November 2023
- Published online by Cambridge University Press:
- 01 April 2022, pp. 2619-2644
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Wild Galois representations: a family of hyperelliptic curves with large inertia image
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 173 / Issue 3 / November 2022
- Published online by Cambridge University Press:
- 26 January 2022, pp. 619-633
- Print publication:
- November 2022
-
- Article
- Export citation
TRUNCATED AFFINE SPRINGER FIBERS AND ARTHUR’S WEIGHTED ORBITAL INTEGRALS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 22 / Issue 4 / July 2023
- Published online by Cambridge University Press:
- 10 November 2021, pp. 1757-1818
- Print publication:
- July 2023
-
- Article
- Export citation
ON SOME CONSEQUENCES OF A THEOREM OF J. LUDWIG
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 3 / May 2022
- Published online by Cambridge University Press:
- 27 September 2021, pp. 1067-1106
- Print publication:
- May 2022
-
- Article
-
- You have access
- Open access
- Export citation
IHARA LEMMA AND LEVEL RAISING IN HIGHER DIMENSION
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 21 / Issue 5 / September 2022
- Published online by Cambridge University Press:
- 25 January 2021, pp. 1701-1726
- Print publication:
- September 2022
-
- Article
- Export citation
Sup-norms of eigenfunctions in the level aspect for compact arithmetic surfaces, II: newforms and subconvexity
- Part of
-
- Journal:
- Compositio Mathematica / Volume 156 / Issue 11 / November 2020
- Published online by Cambridge University Press:
- 15 December 2020, pp. 2368-2398
- Print publication:
- November 2020
-
- Article
- Export citation