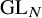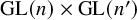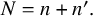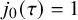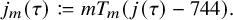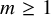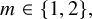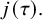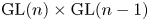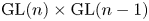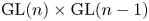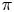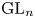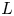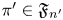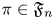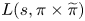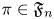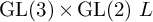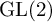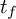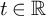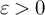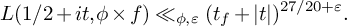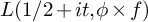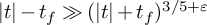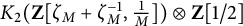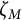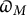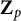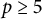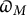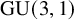Refine search
Actions for selected content:
76 results
Subspaces spanned by eigenforms with nonvanishing twisted central L-values
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 03 October 2025, pp. 1-34
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Klingen Eisenstein congruences and modularity
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 24 September 2025, pp. 1-35
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
p-adic interpolation of Gauss–Manin connections on nearly overconvergent modular forms and p-adic L-functions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 161 / Issue 9 / September 2025
- Published online by Cambridge University Press:
- 05 November 2025, pp. 2380-2441
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Bianchi modular forms and the rationality of periods
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 07 August 2025, pp. 1-19
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Arithmetic Transfer for inner forms of
 $GL_{2n}$
$GL_{2n}$
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 04 August 2025, e128
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EISENSTEIN COHOMOLOGY FOR ORTHOGONAL GROUPS AND THE SPECIAL VALUES OF L-FUNCTIONS FOR
 $\mathrm {GL}_1 \times \mathrm {O}(2n)$
$\mathrm {GL}_1 \times \mathrm {O}(2n)$
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 24 / Issue 6 / November 2025
- Published online by Cambridge University Press:
- 28 July 2025, pp. 2463-2522
- Print publication:
- November 2025
-
- Article
- Export citation
On the Fitting ideals of anticyclotomic Selmer groups of elliptic curves with good ordinary reduction
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 14 July 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Congruent elliptic curves and the
 $\tau $-component in the Iwasawa main conjecture
$\tau $-component in the Iwasawa main conjecture
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 2 / September 2025
- Published online by Cambridge University Press:
- 29 May 2025, pp. 373-408
- Print publication:
- September 2025
-
- Article
- Export citation
Eisenstein Cohomology for
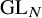 $\mathrm {GL}_N$ and the special values of Rankin–Selberg L-functions over a totally imaginary number field
$\mathrm {GL}_N$ and the special values of Rankin–Selberg L-functions over a totally imaginary number field
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 13 / 2025
- Published online by Cambridge University Press:
- 22 May 2025, e86
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
L-series for Vector-Valued Weakly Holomorphic Modular Forms and Converse Theorems
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 21 January 2025, pp. 1-26
-
- Article
- Export citation
Eichler–Selberg relations for singular moduli
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 12 / 2024
- Published online by Cambridge University Press:
- 10 December 2024, e117
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
On the Gross–Prasad conjecture with its refinement for (SO(5), SO(2)) and the generalized Böcherer conjecture
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 9 / September 2024
- Published online by Cambridge University Press:
- 13 September 2024, pp. 2115-2202
- Print publication:
- September 2024
-
- Article
- Export citation
Period relations for Rankin–Selberg convolutions for
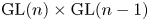 ${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$
${\mathrm {GL}}(n)\times {\mathrm {GL}}(n-1)$
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 8 / August 2024
- Published online by Cambridge University Press:
- 11 September 2024, pp. 1871-1915
- Print publication:
- August 2024
-
- Article
- Export citation
Zeros of Rankin–Selberg L-functions in families
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 5 / May 2024
- Published online by Cambridge University Press:
- 03 April 2024, pp. 1041-1072
- Print publication:
- May 2024
-
- Article
- Export citation
Eisenstein congruences among Euler systems
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 06 November 2023, pp. 425-446
- Print publication:
- June 2024
-
- Article
- Export citation
UNIFORM BOUNDS FOR
 $\operatorname {GL}(3)\times \operatorname {GL}(2)$ L-FUNCTIONS
$\operatorname {GL}(3)\times \operatorname {GL}(2)$ L-FUNCTIONS
- Part of
-
- Journal:
- Journal of the Institute of Mathematics of Jussieu / Volume 23 / Issue 4 / July 2024
- Published online by Cambridge University Press:
- 17 October 2023, pp. 1607-1650
- Print publication:
- July 2024
-
- Article
- Export citation
Concentration of closed geodesics in the homology of modular curves
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 11 / 2023
- Published online by Cambridge University Press:
- 05 October 2023, e91
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Level compatibility in Sharifi’s conjecture
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 11 April 2023, pp. 1194-1212
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Algebraicity of L-values attached to quaternionic modular forms
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 76 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 30 March 2023, pp. 638-679
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Iwasawa–Greenberg main conjecture for nonordinary modular forms and Eisenstein congruences on GU(3,1)
- Part of
-
- Journal:
- Forum of Mathematics, Sigma / Volume 10 / 2022
- Published online by Cambridge University Press:
- 15 December 2022, e110
-
- Article
-
- You have access
- Open access
- HTML
- Export citation