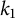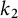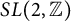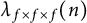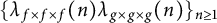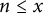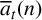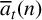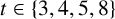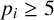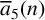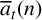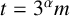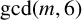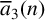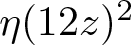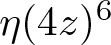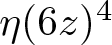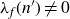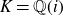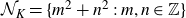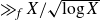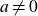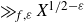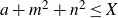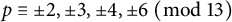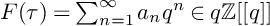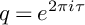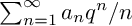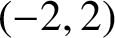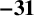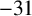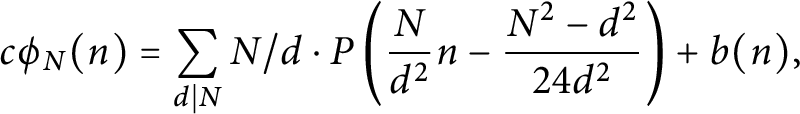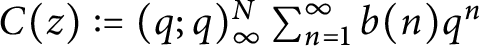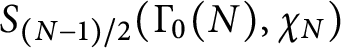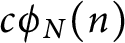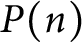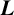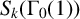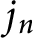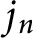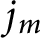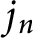Refine search
Actions for selected content:
80 results
Murmurations of modular forms and p-power coefficients
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society , First View
- Published online by Cambridge University Press:
- 26 August 2025, pp. 1-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Asymptotics and sign patterns of Hecke polynomial coefficients
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 68 / Issue 3 / September 2025
- Published online by Cambridge University Press:
- 21 February 2025, pp. 914-926
- Print publication:
- September 2025
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Theta functions, fourth moments of eigenforms, and the sup-norm problem I
- Part of
-
- Journal:
- Compositio Mathematica / Volume 160 / Issue 12 / December 2024
- Published online by Cambridge University Press:
- 03 April 2025, pp. 2916-2969
- Print publication:
- December 2024
-
- Article
- Export citation
On the sign changes of Dirichlet coefficients of triple product L-functions
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 4 / December 2024
- Published online by Cambridge University Press:
- 14 November 2024, pp. 1092-1106
- Print publication:
- December 2024
-
- Article
- Export citation
ARITHMETIC PROPERTIES OF AN ANALOGUE OF t-CORE PARTITIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 03 June 2024, pp. 68-79
- Print publication:
- February 2025
-
- Article
- Export citation
The Heisenberg covering of the Fermat curve
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 5 / October 2025
- Published online by Cambridge University Press:
- 10 May 2024, pp. 1637-1663
- Print publication:
- October 2025
-
- Article
- Export citation
On the vanishing of the coefficients of CM eta quotients
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 4 / November 2023
- Published online by Cambridge University Press:
- 18 October 2023, pp. 1202-1216
-
- Article
- Export citation
An approximation formula for the shifted cubic moment of automorphic L-functions in the weight aspect
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 77 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 06 September 2023, pp. 715-738
- Print publication:
- June 2025
-
- Article
- Export citation
New mock theta functions and formulas for basic hypergeometric series
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 66 / Issue 3 / August 2023
- Published online by Cambridge University Press:
- 22 August 2023, pp. 868-896
-
- Article
- Export citation
Sign changes of fourier coefficients of holomorphic cusp forms at norm form arguments
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 175 / Issue 3 / November 2023
- Published online by Cambridge University Press:
- 23 May 2023, pp. 539-567
- Print publication:
- November 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Modular forms and some cases of the Inverse Galois Problem
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 2 / June 2023
- Published online by Cambridge University Press:
- 06 September 2022, pp. 568-586
- Print publication:
- June 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
MAGNETIC (QUASI-)MODULAR FORMS
- Part of
-
- Journal:
- Nagoya Mathematical Journal / Volume 248 / December 2022
- Published online by Cambridge University Press:
- 30 May 2022, pp. 849-864
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON FINE SELMER GROUPS AND SIGNED SELMER GROUPS OF ELLIPTIC MODULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 19 April 2022, pp. 419-430
- Print publication:
- June 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTREME VALUES OF THE RANKIN–SELBERG
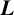 $\boldsymbol {L}$-FUNCTIONS
$\boldsymbol {L}$-FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 21 March 2022, pp. 408-418
- Print publication:
- December 2022
-
- Article
- Export citation
LOWER-ORDER TERMS OF THE ONE-LEVEL DENSITY OF A FAMILY OF QUADRATIC HECKE
 $\boldsymbol {L}$-FUNCTIONS
$\boldsymbol {L}$-FUNCTIONS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 114 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 22 February 2022, pp. 178-221
- Print publication:
- April 2023
-
- Article
- Export citation
AN APPLICATION OF BINARY QUADRATIC FORMS OF DISCRIMINANT
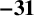 $\boldsymbol {-31}$ TO MODULAR FORMS
$\boldsymbol {-31}$ TO MODULAR FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 269-272
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Torsion properties of modified diagonal classes on triple products of modular curves
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 66 / Issue 1 / March 2023
- Published online by Cambridge University Press:
- 31 January 2022, pp. 68-86
- Print publication:
- March 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
N-colored generalized Frobenius partitions: generalized Kolitsch identities
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 2 / April 2023
- Published online by Cambridge University Press:
- 25 January 2022, pp. 447-469
- Print publication:
- April 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
COUNTING HECKE EIGENFORMS WITH NONVANISHING
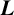 $\boldsymbol {L}$-VALUE
$\boldsymbol {L}$-VALUE
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 1 / August 2022
- Published online by Cambridge University Press:
- 24 January 2022, pp. 28-47
- Print publication:
- August 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Stieltjes interlacing of the zeros of
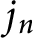 $j_n$
$j_n$
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 4 / December 2022
- Published online by Cambridge University Press:
- 13 January 2022, pp. 976-993
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation