Refine search
Actions for selected content:
29 results
QUANTITATIVE GROWTH OF LINEAR RECURRENCES
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 06 October 2025, pp. 1-34
-
- Article
- Export citation
A NOTE ON THE GENERALISED RAMANUJAN–NAGELL EQUATION
 $x^2=2^m+p^n$
$x^2=2^m+p^n$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 12 September 2025, pp. 1-14
-
- Article
- Export citation
Number of solutions to a special type of unit equations in two unknowns, III
- Part of
-
- Journal:
- Mathematical Proceedings of the Cambridge Philosophical Society / Volume 179 / Issue 3 / November 2025
- Published online by Cambridge University Press:
- 07 August 2025, pp. 737-784
- Print publication:
- November 2025
-
- Article
- Export citation
Multiplicative dependence in linear recurrence sequences
- Part of
-
- Journal:
- Canadian Mathematical Bulletin , First View
- Published online by Cambridge University Press:
- 21 April 2025, pp. 1-11
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON PERFECT POWERS AS SUMS OR DIFFERENCES OF TWO k-GENERALISED PELL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 112 / Issue 2 / October 2025
- Published online by Cambridge University Press:
- 20 January 2025, pp. 227-236
- Print publication:
- October 2025
-
- Article
- Export citation
A MORDELL–LANG-TYPE PROBLEM FOR
 $\mathrm{GL}_{m}$
$\mathrm{GL}_{m}$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 04 October 2024, pp. 433-444
- Print publication:
- June 2025
-
- Article
- Export citation
ON THE DIOPHANTINE EQUATION
 $(P^{(k)}_n)^2+(P^{(k)}_{n+1})^2=P^{(k)}_m$
$(P^{(k)}_n)^2+(P^{(k)}_{n+1})^2=P^{(k)}_m$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 110 / Issue 2 / October 2024
- Published online by Cambridge University Press:
- 06 March 2024, pp. 211-215
- Print publication:
- October 2024
-
- Article
- Export citation
A NOTE ON THE GOORMAGHTIGH EQUATION CONCERNING DIFFERENCE SETS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 23 June 2023, pp. 443-452
- Print publication:
- June 2024
-
- Article
- Export citation
ON A CONJECTURE CONCERNING THE NUMBER OF SOLUTIONS TO
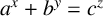 $a^x+b^y=c^z$
$a^x+b^y=c^z$
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 11 November 2022, pp. 40-49
- Print publication:
- August 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
D-finite multivariate series with arithmetic restrictions on their coefficients
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 75 / Issue 6 / December 2023
- Published online by Cambridge University Press:
- 03 October 2022, pp. 1745-1779
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON THE NUMBER OF SOLUTIONS OF TERNARY PURELY EXPONENTIAL DIOPHANTINE EQUATIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 107 / Issue 1 / February 2023
- Published online by Cambridge University Press:
- 10 June 2022, pp. 53-65
- Print publication:
- February 2023
-
- Article
- Export citation
ON REPUNIT CULLEN NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 264-268
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOLUTIONS TO A LEBESGUE–NAGELL EQUATION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 24 May 2021, pp. 19-30
- Print publication:
- February 2022
-
- Article
- Export citation
On the Skolem problem and some related questions for parametric families of linear recurrence sequences
- Part of
-
- Journal:
- Canadian Journal of Mathematics / Volume 74 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 08 February 2021, pp. 773-792
- Print publication:
- June 2022
-
- Article
- Export citation
A NOTE ON JEŚMANOWICZ’ CONJECTURE CONCERNING NONPRIMITIVE PYTHAGOREAN TRIPLES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 1 / August 2021
- Published online by Cambridge University Press:
- 21 October 2020, pp. 29-39
- Print publication:
- August 2021
-
- Article
- Export citation
THE EXPONENTIAL DIOPHANTINE PROBLEM FOR
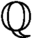 ${\mathbb {Q}}$
${\mathbb {Q}}$
- Part of
-
- Journal:
- The Journal of Symbolic Logic / Volume 85 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 21 July 2020, pp. 671-672
- Print publication:
- June 2020
-
- Article
- Export citation
FAMILIES OF THUE EQUATIONS ASSOCIATED WITH A RANK ONE SUBGROUP OF THE UNIT GROUP OF A NUMBER FIELD
- Part of
-
- Journal:
- Mathematika / Volume 63 / Issue 3 / 2017
- Published online by Cambridge University Press:
- 29 November 2017, pp. 1060-1080
- Print publication:
- 2017
-
- Article
- Export citation
Jeśmanowicz’ Conjecture with Congruence Relations. II
-
- Journal:
- Canadian Mathematical Bulletin / Volume 57 / Issue 3 / 01 September 2014
- Published online by Cambridge University Press:
- 20 November 2018, pp. 495-505
- Print publication:
- 01 September 2014
-
- Article
-
- You have access
- Export citation
PERFECT POWERS WITH THREE DIGITS
- Part of
-
- Journal:
- Mathematika / Volume 60 / Issue 1 / January 2014
- Published online by Cambridge University Press:
- 06 August 2013, pp. 66-84
- Print publication:
- January 2014
-
- Article
- Export citation
ON THE DIOPHANTINE EQUATION x2 + d2l + 1 = yn
-
- Journal:
- Glasgow Mathematical Journal / Volume 54 / Issue 2 / May 2012
- Published online by Cambridge University Press:
- 29 March 2012, pp. 415-428
- Print publication:
- May 2012
-
- Article
-
- You have access
- Export citation







































































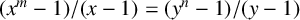
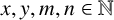
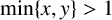
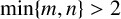
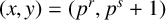
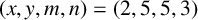
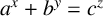
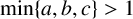
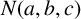
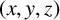
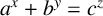


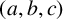
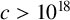
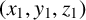
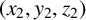
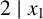
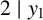
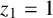
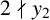
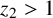
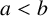
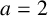
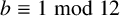
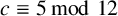
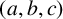
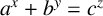
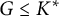
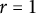
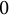
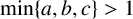
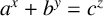
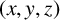
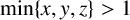
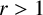
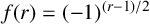
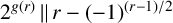
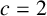
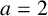
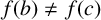
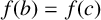
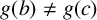
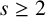
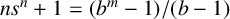
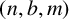
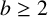
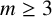
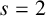
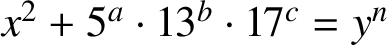
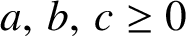
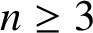
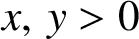
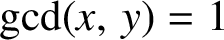
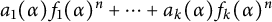

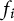
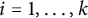
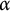

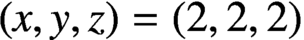
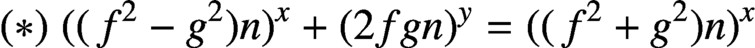
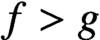
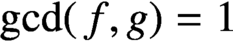
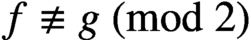
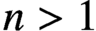
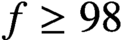
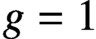

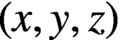
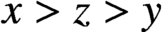
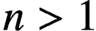
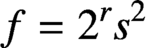
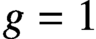
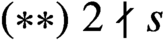
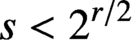

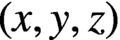
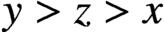
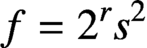
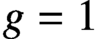

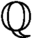
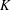
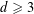
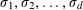
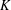
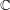

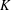
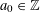
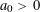
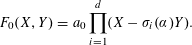

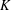
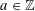
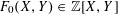
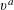
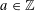

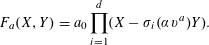
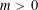
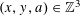
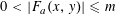
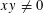
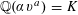
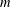
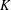
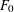

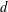

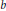

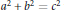

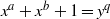
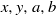
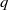
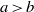
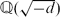 . It is well known (see e.g. [
. It is well known (see e.g. [