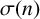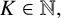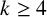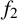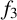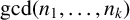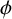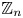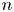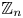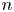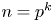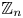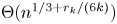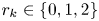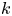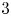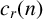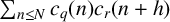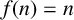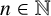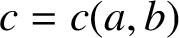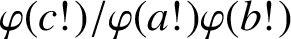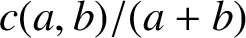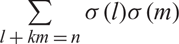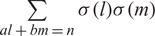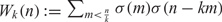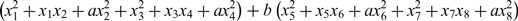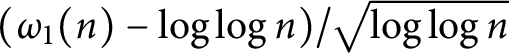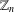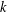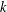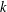Refine search
Actions for selected content:
30 results
DIVISIBILITY AMONG POWER GCD MATRICES AND POWER LCM MATRICES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society , First View
- Published online by Cambridge University Press:
- 01 September 2025, pp. 1-13
-
- Article
- Export citation
Oscillation results for the summatory functions of fake
 $\mu $’s
$\mu $’s
- Part of
-
- Journal:
- Canadian Journal of Mathematics , First View
- Published online by Cambridge University Press:
- 15 August 2025, pp. 1-44
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON SOME EFFECTIVE RESULTS INVOLVING ZEROS OF THE RIEMANN ZETA FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 3 / June 2025
- Published online by Cambridge University Press:
- 21 March 2025, pp. 563-565
- Print publication:
- June 2025
-
- Article
-
- You have access
- HTML
- Export citation
Mean values of multiplicative functions and applications to residue-class distribution
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 68 / Issue 3 / August 2025
- Published online by Cambridge University Press:
- 10 February 2025, pp. 712-730
-
- Article
- Export citation
ON A PROBLEM OF PONGSRIIAM ON THE SUM OF DIVISORS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 1 / February 2025
- Published online by Cambridge University Press:
- 13 September 2024, pp. 13-18
- Print publication:
- February 2025
-
- Article
- Export citation
MULTIPLICATIVE FUNCTIONS k-ADDITIVE ON GENERALISED OCTAGONAL NUMBERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 111 / Issue 2 / April 2025
- Published online by Cambridge University Press:
- 27 August 2024, pp. 212-222
- Print publication:
- April 2025
-
- Article
- Export citation
On theorems of Fermat, Wilson, and Gegenbauer
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 67 / Issue 2 / June 2024
- Published online by Cambridge University Press:
- 12 September 2023, pp. 304-317
- Print publication:
- June 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON SUMS INVOLVING THE EULER TOTIENT FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 3 / June 2024
- Published online by Cambridge University Press:
- 24 August 2023, pp. 486-497
- Print publication:
- June 2024
-
- Article
- Export citation
ON THE ITERATES OF THE SHIFTED EULER’S FUNCTION
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 12 May 2023, pp. 206-214
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON NEAR-PERFECT NUMBERS OF SPECIAL FORMS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 14 February 2023, pp. 366-372
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Discrepancy in modular arithmetic progressions
- Part of
-
- Journal:
- Compositio Mathematica / Volume 158 / Issue 11 / November 2022
- Published online by Cambridge University Press:
- 01 December 2022, pp. 2082-2108
- Print publication:
- November 2022
-
- Article
- Export citation
AFFINE CONVOLUTIONS, RAMANUJAN–FOURIER EXPANSIONS AND SOPHIE GERMAIN PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 1 / August 2023
- Published online by Cambridge University Press:
- 25 October 2022, pp. 11-18
- Print publication:
- August 2023
-
- Article
- Export citation
ON A
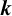 $\boldsymbol {k}$-ADDITIVE UNIQUENESS SET FOR MULTIPLICATIVE FUNCTIONS
$\boldsymbol {k}$-ADDITIVE UNIQUENESS SET FOR MULTIPLICATIVE FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 2 / October 2022
- Published online by Cambridge University Press:
- 08 February 2022, pp. 209-214
- Print publication:
- October 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON QUOTIENTS OF VALUES OF EULER’S FUNCTION ON FACTORIALS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 3 / June 2022
- Published online by Cambridge University Press:
- 17 November 2021, pp. 353-364
- Print publication:
- June 2022
-
- Article
- Export citation
A PROOF OF MERCA’S CONJECTURES ON SUMS OF ODD DIVISOR FUNCTIONS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 2 / April 2022
- Published online by Cambridge University Press:
- 10 September 2021, pp. 197-201
- Print publication:
- April 2022
-
- Article
- Export citation
EVALUATION OF CONVOLUTION SUMS
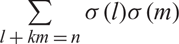 $$\sum\limits_{l + km = n} {\sigma (l)\sigma (m)} $$ AND
$$\sum\limits_{l + km = n} {\sigma (l)\sigma (m)} $$ AND 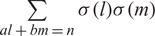 $$\sum\limits_{al + bm = n} {\sigma (l)\sigma (m)} $$ FOR k = a · b = 21, 33, AND 35
$$\sum\limits_{al + bm = n} {\sigma (l)\sigma (m)} $$ FOR k = a · b = 21, 33, AND 35
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 64 / Issue 2 / May 2022
- Published online by Cambridge University Press:
- 16 July 2021, pp. 434-453
- Print publication:
- May 2022
-
- Article
- Export citation
Number of prime factors with a given multiplicity
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 65 / Issue 1 / March 2022
- Published online by Cambridge University Press:
- 03 May 2021, pp. 253-269
- Print publication:
- March 2022
-
- Article
- Export citation
AN EXTENSION OF A RESULT OF ERDŐS AND ZAREMBA
- Part of
-
- Journal:
- Glasgow Mathematical Journal / Volume 63 / Issue 1 / January 2021
- Published online by Cambridge University Press:
- 13 May 2020, pp. 193-222
- Print publication:
- January 2021
-
- Article
- Export citation
THE NUMBER OF CYCLIC SUBGROUPS OF FINITE ABELIAN GROUPS AND MENON’S IDENTITY
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 101 / Issue 2 / April 2020
- Published online by Cambridge University Press:
- 17 May 2019, pp. 201-206
- Print publication:
- April 2020
-
- Article
-
- You have access
- Export citation
ALTERNATING COLOURINGS OF THE VERTICES OF A REGULAR POLYGON
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 2 / October 2019
- Published online by Cambridge University Press:
- 13 February 2019, pp. 177-181
- Print publication:
- October 2019
-
- Article
-
- You have access
- Export citation